Matematické Fórum

LucyLu · 19. 01. 2013 10:36

Ahojky, prosím Vás, máme zadání: rozhodně o lineární závislosti či nezávislosti vektorů...
jdou mi počítat všechny typy, až na jeden typ, a to:

a= (2,3,-1); b= (0,-2,4)

tzn.

2 0
3 -2
-1 4

Mně vyšlo, že jsou lineárně závislé, může mi někdo, prosím Vás, poradit, proč je ve výsledcích LNZ?

Děkuji...:)

Hanis · 19. 01. 2013 10:52

Ahoj,
protože jsi počítala špatně.

Muselo by mj. platit že a(2,3,-1)=(0,-2,4), tj.
2a=0
3a=-2
-a=4

Z první rovnice a=0, z dalších něco jiného, což je spor, tedy jsou LNZ.

LucyLu · 19. 01. 2013 10:58

↑ Hanis: Já se to snažím vypočítat přes Pivoty a nevychází mi to... přes matici a dát ji do schodovitého tvaru...

Hanis · 19. 01. 2013 11:00

No tak to můžeš, ale když sem nedáš postup, tak těžko najdu chybu.

LucyLu · 19. 01. 2013 11:06

↑ Hanis: děkuji, už píšu...

2 0
3 -2
-1 4

dvojku jsem si určila jako Pivot a vynásobila jsem ho TROJKOU a druhý řádek DVOJKOU a odečetla jsem je... tzn.

2 0
0 4
0 8

potom jsem si jako pivot určila ČTYŘKU, vynásobila jsem ho DVOJKOU a odečetla jsem druhý s třetím řádkem, tzn

2 0
0 4
0 0

Hanis · 19. 01. 2013 11:18

To je ok, a co dál?

LucyLu · 19. 01. 2013 11:21

↑ Hanis: no a nám říkali, že když jsou dole nuly, tak je to lineárně závislé... což by v tomto případě znamenalo lineární závislost...
ale jak se na to dívám, není to tak, že by musely být nuly i v tom druhém (prostředím) řádku? protože jsou dvě neznámé?
děkuji.:)

Hanis · 19. 01. 2013 11:23

Ano, dívej se na to jako na řešení soustavy rovnic s nulovou pravou stranou.
Pokud ti vyjde řešení pouze nuly, pak jsou LNZ, jako tady.

LucyLu · 19. 01. 2013 11:26

↑ Hanis: tak teď jsem zmatená, když mám dole dvě nuly, jak jsem psala, tak nám říkali, že je to LINEÁRNĚ ZÁVISLÉ...

LucyLu · 19. 01. 2013 11:29

Myslím to tak, že když:

2 0 ...0
0 4 ...0
0 0 ...0 .... tady mám 0=0 takže LZ...

ale jde o to, jestli při dvou neznámých by to nemělo být:

2 0
0 0
0 0
že by tam ta čtyřka nebyla... a ve druhém řádku by to bylo tedy 0=0, tzn. LZ, v našem případě je tam ale 4=0, tzn LNZ

((:-)) · 19. 01. 2013 11:34 — Editoval ((:-)) (19. 01. 2013 11:36)

↑ LucyLu:

Áno, nejako tak ...

Ináč - ide o dva vektory a= (2,3,-1); b= (0,-2,4).

Tie sú LZ, ak existuje také k, že a = k.b, teda 2 = k.0, súčasne 3 = k.(-2) a -1= k.4

Ale už z prvého vzťahu vyjde, že k neexistuje, takže LZ nie sú, takže sú LN.

A keď už matica, nerozumiem, prečo stĺpce, keď stačili riadky a na nich tá nezávislosť bola vidieť okamžite...

standyk · 19. 01. 2013 11:43

↑ LucyLu:

Aká je hodnosť tej matice ktorú si dostala po tých úpravách? Teraz porovnaj tú hodnosť s počtom vektorov. Ak sa rovnajú tak sú lineárne nezávislé.
Možno trochu pritiahnuté za vlasy ale: Ak by si mala len jeden vektor a zapíšeš ho ako maticu a upravuješ na schodovitý tvar, tak by si dostala maticu tvaru: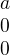
$\begin{matrix} a \\ 0 \\ 0 \end{matrix}$
a vtedy by si tiež prehlásila že ten jeden vektor je lineárne závislý?

LucyLu · 19. 01. 2013 11:45

↑ standyk: asi ne, děkuji Vám... :)

LukasM · 19. 01. 2013 15:47

LucyLu napsal(a):
Myslím to tak, že když:

2 0 ...0
0 4 ...0
0 0 ...0 .... tady mám 0=0 takže LZ...

ale jde o to, jestli při dvou neznámých by to nemělo být:

2 0
0 0
0 0
že by tam ta čtyřka nebyla... a ve druhém řádku by to bylo tedy 0=0, tzn. LZ, v našem případě je tam ale 4=0, tzn LNZ

Tohle je celé blbost. Tam není žádné 0=0 nebo 4=0, na levé straně jsou koeficienty u nějaké neznámé. Takže Například ta první matice soustavy odpovídá rovnicím
$2a+0b=0\\0a+4b=0\\0a+0b=0$
Takže je jasně vidět, že a=b=0. Proto jsou vektory lineárně nezávislé.

Ve druhém případě (kdyby ti po úpravách vyšla takováhle matice soustavy) je nutné, aby a=0, ale b můžeš zvolit libovolně. Proto by vektory byly lineárně závislé.

LucyLu · 20. 01. 2013 11:14

↑ LukasM: Tak to nechápu.
Nás učili pomocí matic, ne rovnic, rovnice nechápu a ani chápat asi nebudu a zajímalo by mne, jak je to s těmi maticemi, protože když pak počítám bázi...

Hanis · 20. 01. 2013 11:25

Matice je totéž, co soustava rovnic.

LucyLu · 20. 01. 2013 12:15

↑ Hanis:
Takže když to dám do matice a počítám přes pivoty a výjdou mi tam nulové řádky, tak je to jak, prosím Vás?

Hanis · 20. 01. 2013 12:27

Tady nejde o nulové řádky v matici, tady jde o řešení soustavy rovnic. Najdi si nejprve někde definici lineární (ne)závislosti, ať víš, o čem se bavíme.

LucyLu · 20. 01. 2013 12:30

↑ Hanis:
Já vím, že o co go... ale říkám, že to neumím přes rovnici... že jsme se to učili počítat pomocí matice... vím, že tam je ta podmínka, že se lin. kombinace vektorů musí rovnat nule, aby byly lin.závislé...
to chápu, ale i tak to dělám tak, že si to hodím do matice...:)

Hanis · 20. 01. 2013 14:31

Já o koze, ty o voze.

Snad ti poradí někdo jiný, já se ti snažím vysvětlit že matice je ta soustava rovnic.

((:-)) · 20. 01. 2013 14:44 — Editoval ((:-)) (20. 01. 2013 14:54)

↑ LucyLu:

Pri riešení rovníc sčítacou metódou (teda Gaussovou eliminačnou metódou) rovnice upravuješ tak, aby pod sebou vznikol rovnaký počet rovnakých písmeniek s opačnými znamienkami.

Ak treba, rovnice upravuješ tak, aby po zlúčení niektorá neznáma vypadla:

$x+y+z=3\\x-y+z=1\\x+y-z=1$

Odčítaš od prvej rovnice druhú, vypadne x a z. Odčítaš od prvej tretiu, vypadne x aj y:

$x+y+z&=1\\0x+2y+0z&=2\\0x+0y+2z&=2$

Z poslednej rovnice: z = 1, z druhej y = 1 a po dosadení týchto hodnôt do prvej x = 1.

Toto isté môžeš robiť pomocou úpravy matíc. Neznáme si "pamätáš" a píšeš iba čísla pri nich, pritom úpravy robíš presne tie isté ako s rovnicami, len neznáme (písmenká) priamo nevypisuješ.

$\left( \begin{array}{ccc@{\ }r} 1 & 1 & 1 &| 3 \\ 1 & -1 & 1 &|1 \\ 1 & 1 &-1\ \ & |1 \ \end{array} \right)$

Upravíš, aby v 1. stĺpci boli pod 1 nuly (ako keď odčítaš rovnice)

$\left( \begin{array}{ccc@{\ }r} 1 & 1 & 1 &| 3 \\ 0 & 2 & 0 &|2 \\ 0 & 0 & 2 &|2 \ \end{array} \right)$

Posledný riadok sa prevedie do reči rovníc a znamená, že 2z=2, teda z = 1 a tak ďalej...

Matematické Fórum

#1 19. 01. 2013 10:36

Lineární závislost/ nezávislost?

#2 19. 01. 2013 10:52

Re: Lineární závislost/ nezávislost?

#3 19. 01. 2013 10:58

Re: Lineární závislost/ nezávislost?

#4 19. 01. 2013 11:00

Re: Lineární závislost/ nezávislost?

#5 19. 01. 2013 11:06

Re: Lineární závislost/ nezávislost?

#6 19. 01. 2013 11:18

Re: Lineární závislost/ nezávislost?

#7 19. 01. 2013 11:21

Re: Lineární závislost/ nezávislost?

#8 19. 01. 2013 11:23

Re: Lineární závislost/ nezávislost?

#9 19. 01. 2013 11:26

Re: Lineární závislost/ nezávislost?

#10 19. 01. 2013 11:29

Re: Lineární závislost/ nezávislost?

#11 19. 01. 2013 11:34 — Editoval ((:-)) (19. 01. 2013 11:36)

Re: Lineární závislost/ nezávislost?

#12 19. 01. 2013 11:43

Re: Lineární závislost/ nezávislost?

#13 19. 01. 2013 11:45

Re: Lineární závislost/ nezávislost?

#14 19. 01. 2013 15:47

Re: Lineární závislost/ nezávislost?

LucyLu napsal(a):

#15 20. 01. 2013 11:14

Re: Lineární závislost/ nezávislost?

#16 20. 01. 2013 11:25

Re: Lineární závislost/ nezávislost?

#17 20. 01. 2013 12:15

Re: Lineární závislost/ nezávislost?

#18 20. 01. 2013 12:27

Re: Lineární závislost/ nezávislost?

#19 20. 01. 2013 12:30

Re: Lineární závislost/ nezávislost?

#20 20. 01. 2013 14:31

Re: Lineární závislost/ nezávislost?

#21 20. 01. 2013 14:44 — Editoval ((:-)) (20. 01. 2013 14:54)

Re: Lineární závislost/ nezávislost?

Zápatí