Matematické Fórum

jardofpr · 19. 01. 2013 23:58

ahojte
len taká otázka:

veta tvrdí, že ak sú 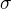$(X,\mathcal{A},\nu)\,,\,(Y,\mathcal{B},\mu)$ $\sigma$ -konečné priestory a pre merateľnú funkciu $f:X\times Y \rightarrow \mathbb{C}$ platí $f \in L^1(X\times Y,\nu \times \mu):=\{g:X\times Y \rightarrow \mathbb{C}\,:\,\int_{X\times Y}|g(x,y)|\mathrm{d}(\nu\times\mu)<\infty\}$

tak platí $\int_{X\times Y}f\mathrm{d}(\nu\times\mu)=\int_{X}\int_{Y}f\mathrm{d}\mu\mathrm{d}\nu=\int_{Y}\int_{X}f\mathrm{d}\nu\mathrm{d}\mu$

trochu mi vŕta v hlave ako overiť podmienku $\int_{X\times Y} |f|\mathrm{d}(\nu\times\mu)$ v konkrétnom príklade,

predtým než dôjde k samotnému výpočtu pomocou tvrdenia vety, teda, či je na to nejaký všeobecný postup
alebo záleží od príkladu k príkladu, ono presvedčiť sa priamo že tá podmienka platí nemusí byť vždy jednoduché

vďaka

lecopivo · 20. 01. 2013 00:41

No mam pocit, ze ten predpoklad jde zeslabit. Neni treba aby $\int_{X \times Y} |g(x,y)| d(\nu \times \mu) < \infty$ . Ale staci aby integral $\int_{X \times Y} g(x,y) d(\nu \times \mu)$ existoval(muze byt i +-nekonecno). Tedy jediny pripad, kdy veta nemuze platit je kdyz $\int_{X \times Y} g^+(x,y) d(\nu \times \mu) = \int_{X \times Y} g^-(x,y) d(\nu \times \mu) = \infty$

No a hlavni dva pripady, kdy veta plati, je kdyz g je kladna nebo g je spojita a integrujes pres kompakt.

jardofpr · 20. 01. 2013 03:08

↑ lecopivo:

nie je mi jasné čo sa myslí funkciami $g^+$ a $g^-$ pri komplexnej funkcii $g$

ešte som sa v tom vŕtal a vyzerá to, že by mohlo stačiť aj overiť či sú oba dvojné integrály z $|g|$ konečné

alebo prípadne použiť Tonelliho vetu pre $|g|$ keďže je $|g|\geq 0$

check_drummer · 20. 01. 2013 03:11

↑ jardofpr:
Ahoj, nepomohl by vhodný odhad integrované funkce?

jardofpr · 20. 01. 2013 03:36

ahoj ↑ check_drummer:

no, tie odhady fungujú celkom dobre keď sú $X$ a $Y$ trebárs nejaké intervaly alebo "pekné" podmnožiny v $\mathbb{R}$

všeobecne tam môžem mať iné priestory, preto ma zaujímal nejaký "všeobecnejší recept"

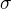lebo už v prípadoch keď je napr. $X=Y=\mathbb{N}$ s potenčnými $\sigma$ -algebrami sa s odhadmi funkcie veľmi pracovať nedá, a môžu tam byť zrejme aj "škaredšie" veci

lecopivo · 20. 01. 2013 10:24

Aha! ja si nevsiml, ze to mas pro komplexni fce. No ale lepsi je to formulovat pro fce realne a pak to aplikovat na realnou a komplexni slozku zvlast. To uz se jedna o vse realne a v nekterych pripadech na ne jde pouzit tu Tonelliho vetu.

↑ jardofpr:

|g| je vzdy nezaporne.

lecopivo · 20. 01. 2013 10:26

A kdyz tak sem hod nejaky priklad. Obecny navod jak postupovat asi neexistuje.

jardofpr · 21. 01. 2013 10:13

↑ lecopivo:

aj som očakával že to tak bude, ale jeden nikdy nevie
aj keď Tonelli zatiaľ funguje celkom dobre tam kde nefungujú odhady funkcií :)

Matematické Fórum

#1 19. 01. 2013 23:58

Fubiniho veta

#2 20. 01. 2013 00:41

Re: Fubiniho veta

#3 20. 01. 2013 03:08

Re: Fubiniho veta

#4 20. 01. 2013 03:11

Re: Fubiniho veta

#5 20. 01. 2013 03:36

Re: Fubiniho veta

#6 20. 01. 2013 10:24

Re: Fubiniho veta

#7 20. 01. 2013 10:26

Re: Fubiniho veta

#8 21. 01. 2013 10:13

Re: Fubiniho veta

Zápatí