Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Semidefinitnosť vs. extrémy (TOTO TÉMA JE VYŘEŠENÉ)
#1 22. 01. 2013 13:05
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Semidefinitnosť vs. extrémy
Zdravím,
mám jednu otázku ohľadom extrémov. Keď ich overujem pomocou matice druhých parciálnych derivácií, viem, že keď je táto matica kladne definitná, tak je príslušný bod lokálne minimum. Dostala som sa ale do bodu, keď mi vyšiel 1x1 subdeterminant rovný 1, 2x2 subdeterminant rovný 0, 3x3 subdeterminant rovný 6. Teraz neviem, či bod, pre ktorý som rátala subdeterminanty, bude extrém alebo nie. Vedel by mi niekto poradiť?
Vopred ďakujem.
Offline
- (téma jako vyřešené označil(a) Blackflower)
#3 22. 01. 2013 14:39
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Semidefinitnosť vs. extrémy
↑ Brano: Čiže keď mám extrémy s väzbou, treba vždy použiť obkolesený hessián?
Offline
#4 22. 01. 2013 14:47 — Editoval Brano (22. 01. 2013 14:48)
Re: Semidefinitnosť vs. extrémy
Och ano to urcite. Ak ho nepouzijes tak mozes dostat priamo nespravny vysledok. Napr.: s vazbou
s vazbou  ma urcite minimum v
ma urcite minimum v  , zatial co "plna"(? - neviem spravny nazov) Hessova matica je
, zatial co "plna"(? - neviem spravny nazov) Hessova matica je
PS: neviem co znamena obkoleseny Hessian, len sa domyslam :-), ja to robim cez kvadraticku formu druheho diferencialu.
Offline
#5 22. 01. 2013 15:16
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Semidefinitnosť vs. extrémy
↑ Brano: "Obkolesený" Hessián je Hessova matica s tým, že sa tam doplnia ešte parciálne derivácie väzby.
Mám príklad:

Postup:
parciálne zderivované, položiť rovné nule, z toho mi vyšlo toto:
Vyšiel mi z toho iba jeden kandidát na extrém, a to ![kopírovat do textarea $A=[1,1,1]$](/mathtex/ee/eeeb4298897ce0da978b67dd4e7b03fd.gif) .
.
Spravila som si Hessove matice:

V tej prvej vychádzajú subdeterminanty 1, 0 a 6, ak sa nemýlim. Druhá je singulárna, čiže určite bude treba použiť obkolesenú maticu, ktorá mi vychádza takto:
Dosadím tam teda môj vypočítaný bod a zistím determinant.
Offline
#6 22. 01. 2013 15:33 — Editoval Brano (22. 01. 2013 15:53)
Re: Semidefinitnosť vs. extrémy
Tych kandidatov na extrem sa mi zda, ze je viac. Konkretne 14.![kopírovat do textarea $[0,0,\pm \sqrt{3}]$](/mathtex/7e/7efc08bd344a2361d837a68a649e7eee.gif) pre
pre 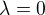 + cyklicke zameny a
+ cyklicke zameny a![kopírovat do textarea $[\pm 1,\pm 1,\pm 1]$](/mathtex/63/6316ed2c2137f00ac95b9d4a12b20174.gif) pre
pre  (vhodne z tej dvojice).
(vhodne z tej dvojice).
A to s tym obkolesenym Hessianom som nepochopil, podla mna by o tom ci sa jedna o extrem mala rozhodnut objekt v tvare matice 2x2 a nie 4x4 kedze uloha ma 2 stupne volnosti.
Ak chces mozem ti napisat svoj postup, ale ten by bol cez tie formy.
Offline
#7 22. 01. 2013 15:37 — Editoval Blackflower (22. 01. 2013 15:37)
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Semidefinitnosť vs. extrémy
↑ Brano: Až 11? Do hája... mne vyšlo iba  ...
...
Offline
#8 22. 01. 2013 15:54 — Editoval Brano (22. 01. 2013 15:56)
Re: Semidefinitnosť vs. extrémy
Este som pridal tri body za znamienka v prvom pripade - uprimnu sustrast - ale ako tak pozeram, tak v nich extremy nie su a ani neviem co tam je, lebo aj redukovana forma 2. diferencialu je semi-definitna - ale vyzera ze aj dalsie diferencialy su nulove, tak by to moholi byt extremy aj ked W|A tvrdi, ze nie
Offline
#9 22. 01. 2013 15:56
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Semidefinitnosť vs. extrémy
↑ Brano: no čo už :D ďakujem veľmi pekne za pomoc, odpoveď na moju prvotnú otázku som dostala a teraz mi ostáva už len veriť, že na skúške takýto príklad nebude :D
Offline
#11 22. 01. 2013 16:11
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Semidefinitnosť vs. extrémy
↑ Brano: Čiže koľko ich nakoniec bude? :)
Offline
#13 22. 01. 2013 16:20
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Semidefinitnosť vs. extrémy
↑ Brano: ešte uvidím, ako na tom budem :) ďakujem za ochotu a trpezlivosť :)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Semidefinitnosť vs. extrémy (TOTO TÉMA JE VYŘEŠENÉ)



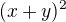
![kopírovat do textarea $[0,0,\sqrt{3}]$](/mathtex/52/5246b3ed7762cd5ea237b2e56d59c2af.gif) su sedlove - redukovany 2.diferencial je indefinitny konkretne pre tento bod mi vysiel
su sedlove - redukovany 2.diferencial je indefinitny konkretne pre tento bod mi vysiel  - ak som tam teda zase nieco nezmrvil.
- ak som tam teda zase nieco nezmrvil.