Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Derivácia vektorového súčinu (TOTO TÉMA JE VYŘEŠENÉ)
#3 23. 01. 2013 10:59 — Editoval Zeck (23. 01. 2013 11:17)
Re: Derivácia vektorového súčinu
Brano napsal(a):
A co z toho su funkcie casu?
myslim ze vsetko su funkcie casu, skusam to vselijak derivovat, ale nijak mi nevychadza, to co by malo, takze pravdepodobne je chyba v tom ze neviem ako derivovat taketo vektorove veci.
Vyjsť by malo toto:![kopírovat do textarea $\frac{\mathrm{d} }{\mathrm{d}t }[\vec{\omega }* (\xi .\vec{i}+\eta .\vec{j})]=\vec{\omega} *(\frac{\mathrm{d} \xi}{\mathrm{d}t }.\vec{i}+\frac{\mathrm{d} \eta}{\mathrm{d}t }.\vec{j})+\vec{\alpha }*(\xi .\vec{i}+\eta.\vec{j})+\vec{\omega} *(\frac{\mathrm{d} \xi}{\mathrm{d}t }.\vec{i}+\frac{\mathrm{d} \eta}{\mathrm{d}t}.\vec{j}+\xi .\frac{\mathrm{d} \vec{i}}{\mathrm{d}t }+\eta .\frac{\mathrm{d} \vec{j}}{\mathrm{d} t})$](/mathtex/16/161473f8f8b7a025fe52a4dcc8d4d544.gif)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Derivácia vektorového súčinu (TOTO TÉMA JE VYŘEŠENÉ)




 a
a 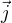 su funkcie casu - co som si myslel, ze nie su.
su funkcie casu - co som si myslel, ze nie su. - je tak?
- je tak?![kopírovat do textarea $\frac{\mathrm{d} }{\mathrm{d}t }[\vec{\omega }\times(\xi .\vec{i}+\eta .\vec{j})]=\vec{\alpha }\times(\xi .\vec{i}+\eta.\vec{j})+\vec{\omega}\times\left(\frac{\mathrm{d} \xi}{\mathrm{d}t }.\vec{i}+\frac{\mathrm{d} \eta}{\mathrm{d}t}.\vec{j}+\xi .\frac{\mathrm{d} \vec{i}}{\mathrm{d}t }+\eta .\frac{\mathrm{d} \vec{j}}{\mathrm{d} t}\right)$](/mathtex/af/af16a1aef8b788ad880fa33e98cec3a7.gif)