Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 21. 01. 2013 18:09
Re: MO - z9 - 12/13
Doplňuji: zadání zde: http://cgi.math.muni.cz/~rvmo/Z/62/Z62-Letak.pdf kategorie Z9. Díky moc
Offline
#3 24. 01. 2013 15:02 — Editoval Blackflower (25. 01. 2013 13:47)
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: MO - z9 - 12/13
↑ kozomelec: Ahoj.
Najprv k príkladu č. 5:
Predstavím si, že na začiatku do schémy doplním číslo x, bez ohľadu na to, aké je. Pozorujem, čo s ním urobia jednotlivé operácie. -> x2 ->
-> x2 -> 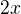 -> :3 ->
-> :3 -> 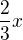 -> x4 ->
-> x4 ->  -> :6 ->
-> :6 -> 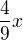 -> x5 ->
-> x5 ->  -> :6 ->
-> :6 ->  -> x3 ->
-> x3 ->  -> :2 ->
-> :2 ->  -> x3 ->
-> x3 ->  -> :2 ->
-> :2 -> 
Teraz potrebujeme dosiahnuť, aby všetky čísla, ktoré nám po operáciách ostanú, boli celé. To znamená, že nech je x akékoľvek, musí byť deliteľné všetkými menovateľmi, čo nám vo výrazoch vznikli, a zároveň keď ho vynásobíme číslom v čitateli, nesmie presiahnuť číslo 9999.
Zapísala by som to asi takto:
-po každej operácii nám vznikne číslo v tvare 
-musí platiť  , teda
, teda 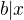 (b delí x)
(b delí x)
-musí platiť 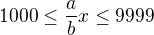
K prvej podmienke: pozrieme sa na všetky menovatele a hľadáme ich najmenší spoločný násobok, aby sme mali zaručené, že číslo x bude po hociktorej operácii. Delitele, čo sa v operáciách vyskytujú, sú 3, 6, 9, 27 (niektoré aj viackrát, ale to nám nevadí). Ich najmenší spoločný násobok je 54, to znamená, že hľadané x musí byť deliteľné 54.
K druhej podmienke: ak chceme, aby platila, stačí nám zaručiť, aby najmenší zo zlomkov, ktorým násobíme číslo x v jednotlivých krokoch, neklesol pod 1000 a aby najväčší nepresiahol 9999. Nájdeme si najväčšie a najmenšie číslo násobiace x a dostávame: , teda
, teda  , berieme
, berieme 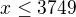 (najbližšie celé číslo)
(najbližšie celé číslo) , teda
, teda 
Ostáva nám zistiť, koľko čísel medzi 2250 a 3749 je deliteľných 54.
Najbližšie číslo deliteľné 54, ktoré je väčšie ako 2250, je 2268: 2268/54=42. Najbližšie číslo deliteľné 54 menšie ako 3479 je 3726=69*54. Stačí teda spočítať, koľko je čísel v intervale <42,69>. To je 28.
Offline
#4 24. 01. 2013 15:18
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: MO - z9 - 12/13
↑ kozomelec: Úloha č.1 mi dala zabrať, ale predsa sa nakoniec podarila.
Najprv som si napísala všeobecné trojciferné číslo (všetky cifry rôzne) a všetky čísla, ktoré sa dajú dostať výmenou číslic:
ABC -> ACB, BAC, BCA, CAB, CBA
Keďže v zadaní sme mali také číslo, kde sme získali iba tri nové trojciferné čísla, skúsila som si napísať číslo, ktoré má 2 cifry rovnaké:
ABB-> BAB, BBA
Tu mi vyšli iba dve rôzne čísla, tak som sa vrátila k prvému prípadu a povedala som si, že čo ak bude jedna z cifier nula?
AB0->0AB, 0BA, B0A, BA0, A0B
Čísla 0AB a 0BA nie sú trojciferné, keďže nula z nich urobí iba dvojciferné, takže z toho viem, že hľadané číslo bude obsahovať nulu.
Máme teda čísla AB0, BA0, A0B, B0A. Ideme hľadať dve najmenšie. Rozdelila som si to na dva prípady:
1.) A<B - dve najmenšie čísla budú A0B, AB0
2.) A>B - dve najmenšie čísla budú B0A, A0B
Vidím, že majú rovnaký tvar, takže vo všeobecnosti je jedno, ktoré zoberiem. Ja som sa rozhodla pracovať s tou prvou dvojicou.
Každé trojciferné číslo XYZ sa dá napísať takto: XYZ=100X+10Y+Z, rozpíšeme si teda aj naše nájdené čísla:
(100A+10*0+B)+(100A+10B+0*1)=100*2A+10B+B=100*10+10*8+8=1088 (rozpísala som si aj súčet čísel, ktorý je daný)
Výraz na ľavej strane nám tiež určuje nejaké číslo, ktoré sa musí rovnať pravej strane. Keďže A, B sú číslice (teda jednociferné čísla), musí platiť, že číslica na mieste stoviek napravo sa bude rovnať číslici na mieste stoviek naľavo, číslica na mieste desiatok napravo sa bude rovnať číslici na mieste desiatok naľavo a číslica na mieste jednotiek napravo sa bude rovnať číslici na mieste jednotiek naľavo.
Z toho nám vylezú jednoduché rovnice:
2A=10
B=8 (túto rovnicu dostaneme dokonca dvakrát)
Teda hľadané číslo sa skladá z číslic 0, 5 a 8.
Kontrola:
Z číslic 0, 5, 8 môžeme dostať trojciferné čísla 580, 850, 508 a 805.
Dve najmenšie sú 580 a 508, ich súčet je naozaj 1088, takže úloha je vyriešená.
Offline
#5 25. 01. 2013 03:25
Re: MO - z9 - 12/13
↑ Blackflower:
Tu by som pridal taky medzikrok. Akonahle zistime, ze 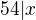 tak si mozme oznacit
tak si mozme oznacit  a prepisat vsetky cleny tej postupnosti ... a potom uz iba najdeme najvacsi a najmensi a zabezpecime aby boli 4-ciferne.
a prepisat vsetky cleny tej postupnosti ... a potom uz iba najdeme najvacsi a najmensi a zabezpecime aby boli 4-ciferne.
Offline
#6 25. 01. 2013 09:32 — Editoval Blackflower (25. 01. 2013 13:47)
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: MO - z9 - 12/13
↑ Brano: Áno, je to lepší spôsob, ten, čo mám v postupe ja, nie je celkom správny. Opravím.
Edit: opravené, dúfam, že tam už nie je žiadna chyba
Offline
