Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Logika - sémantický spor (TOTO TÉMA JE VYŘEŠENÉ)
#1 19. 12. 2012 21:24 — Editoval bsft (19. 12. 2012 21:25)
Logika - sémantický spor
Ahoj, snad jsem zvolil dobrý topic ... ale k problému. 
Zadání říká, že mám použít sémanticky spor, ale ten jsem doteď používal, jen pokud jsem měl v příkladu implikaci, kde jsem mohl znegovat závěr a vycházet z pravdivých předpokladů. Ovšem z tohoto zadání mi není jasné, jak bych to měl dokázat pomocí sémantického sporu. Mohl by mě někdo navést, pokud je zadání v pořádku. Díky.
Offline
- (téma jako vyřešené označil(a) bsft)
#3 20. 12. 2012 17:58 — Editoval bsft (20. 12. 2012 17:58)
Re: Logika - sémantický spor
↑ kexixex:
V mém případě je  implikace. Jinak to, co jsi napsal je špatně, protože pokud se nepletu, tak správně to je takto:
implikace. Jinak to, co jsi napsal je špatně, protože pokud se nepletu, tak správně to je takto: 
Sémantickým sporem, lze ověřit pravdivost úsudku, ovšem já vím, jak to vyřešit, pokud by nějaké předpoklady implikovali závěr. Takto, když mám v zadání jenom konjukce "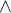 ", tak si nevím rady. :-(
", tak si nevím rady. :-(
Offline
#4 22. 12. 2012 00:59
Re: Logika - sémantický spor
pojem sémantického sporu sice při vyhodnocování neznám ale intuitivně bych to dělal tak co znamená že formule je tautologie , po odpovědi na tuto otázku , si položím otázku , kdy je formule konjunkce pravdivá,
tedy budu u jednom konjuktu uvažovat že je nepravdivý a ukáže toto hodnocení existuje, potom odpověd bude zjevná ne ?
Offline
#5 23. 12. 2012 15:32
Re: Logika - sémantický spor
↑ Mr.Pinker:↑ Mr.Pinker:
Aha ... no pokud předpokládám, že první část s implikací je rovna nule, tak ke sporu dojdu a z toho by mělo plynout, že je to celé tautologie. Ale když jsem si udělal tabulku pro kontrolu, tak to tautologie není ... tautologie je, že pro všechny ohodnocení, by to muselo být pravda a první část rozhodně pravdivá vždy není ... tak teď nevím, co s tím. Potřeboval bych nějak objasnit.
Offline
#8 27. 01. 2013 18:10
Re: Logika - sémantický spor
Metoda sémantickým sporem se dá udělat různými způsoby. Při ověřování tautologičnosti formule můžeme například využít následující postup: Mějme formuli F, tuto formuli znegujeme a nyní její výstup ohodnotíme jako 1 (tedy přiřadíme hodnotu 1 k logické spojce na nejvyšší úrovni). Jestliže NEDOJDEME při některém ohodnocení ke sporu, znamená to, že připouštíme, že negovaná formule vyjde při tomto ohodnocení 1. Původní ne-negovaná formule tedy vyjde 0 a jistě není tautologie...v opačném případě, když u negované formule dojdeme pokaždé ke sporu, znamená to, že původní formule je tautologie.
Zkuste si to s původním příkladem. Znegujeme formuli, obě konjunkce se změní na disjunkce, jednotlivé disjunkty se znegují...aby vyšla formule celkově jako 1, stačí, aby jediný disjunkt měl hodnotu 1. Dejme tomu ten prostřední disjunkt (p \wedge q') - tedy konjunkce těchto dvou literálů vyjde 1...ostatní disjunkty vyjdou 0. Nyní přiřazujeme jednotlivé ohodnocení výrokovým symbolům. Velmi rychle si ověříme, že ke sporu zde nedojde, tedy připouštíme to, že negovaná formule může při jistém ohodnocení vyjít 1...původní formule tedy při tomto ohodnocení vyjde 0...tzn. původní formule není tautologií.
Offline
#9 27. 01. 2013 18:13
Re: Logika - sémantický spor
jinak sémantický spor znamená v podstatě to, že se snažíme dojít ke sporu tím, že přiřazujeme skutečné hodnoty jednotlivým výrokovým symbolům. Nepracujeme tedy čistě s formulí samotnou - její strukturou, ale se skutečným ohodnocením - tedy významem - sémantikou.
Offline
#10 29. 01. 2013 20:46
Re: Logika - sémantický spor
↑ chim_chim:
Díky moc, teď už mi je sémantický spor zcela jasný, po tomto výkladu, který jsem tak hledal.
Offline
#11 31. 01. 2013 10:20
Re: Logika - sémantický spor
Prosím. Samozřejmě to jde i přímo, chtěl jsem jen ukázat, že možností je více a problém není naučit se techniku, ta je více než jednoduchá, ale jde o to, pochopit princip.
Přímý způsobem bychom ohodnotili danou formuli jako 0 a snažili se prostě (ne)dojít ke sporu. Stačí jediný případ, kdy bychom ke sporu nedošli a formule nemůže být tautologie, protože ta musí být jistě pravdivá při všech valuacích;)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Logika - sémantický spor (TOTO TÉMA JE VYŘEŠENÉ)
 , mozna preklep?) ale urcite lze pomoci negace a implikace vyrok prepsat...
, mozna preklep?) ale urcite lze pomoci negace a implikace vyrok prepsat...

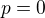 a
a  a už máš konkrétní ohodnocení, při němž není formule pravdivá.
a už máš konkrétní ohodnocení, při němž není formule pravdivá.