Matematické Fórum

misickacz · 14. 12. 2008 15:55

Ahojky, potřebuji poradit s příkladem:

Na každé z planet planetárního systému je astronom, který pozoruje nejbližší planetu, každé 2 vzdálenosti planet jsou různé. Dokažte, že když je počet planet lichý, pak některou planetu žádný astronom nepozoruje.

Vím, že se to má řešit matematickým důkazem, nejspíš matemat. indukcí, ale nevím konkrétně jak.
Předem děkuji za pomoc.

Kondr · 14. 12. 2008 16:58

Pro spor předpokládejme, že planet je lichý počet a každou někdo pozoruje.

Uvažme orientovaný graf, jehož vrcholy jsou planety a hrana z A do B vede pokud astronom z planety A pozoruje planetu B. Výstupní stupně všech vrcholů jsou 1. Pokud by každá planeta byla pozorována, byl by vstupní stupeň každého vrcholu také 1, graf by byl tvořen cykly. Pokud by byl počet planet lichý, měl by některý cyklus délku alespoň tři. Nechť (C,D) je nejkratší hrana tohoto cyklu. Protože má cyklus délku alespoň 3, astronom z planety D nepozoruje C, takže nepozoruje k sobě nejbližší planetu, spor.

Jak do toho nějak efektivně zapojit indukci nevím. Můj "důkaz" je spíš nástin, je potřeba některé části zdůvodnit.

Pavel · 14. 12. 2008 18:33 — Editoval Pavel (14. 12. 2008 19:24)

Já bych na to šel takto. Nechť je dán lichý počet planet $n$ a předpokládejme, že každá planeta je viděna právě jedním astronomem. Označme planety následujícím způsobem:

- zvolme libovolnou planetu a označme ji 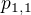$p_{1,1}$ .

Nyní mohou nastat dvě možnosti:
1. Nechť astronom na planetě 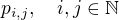$p_{i,j},\quad i,j\in\mathbb N$ vidí planetu, která ještě nebyla označena. Pak tuto planetu označme symbolem $p_{i,j+1}$ .

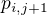2. Nechť astronom na planetě 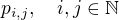$p_{i,j},\quad i,j\in\mathbb N$ vidí planetu, která již označena byla. Pak symbolem 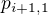$p_{i+1,1}$ označme kteroukoliv jinou planetu, která zatím označena nebyla.

Celý postup opakujme, dokud nebudou označeny všechny planety.

Definujme množinu 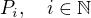$P_i,\quad i\in\mathbb N$ jako množinu těch planet, které jsme označili symbolem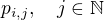 $p_{i,j},\quad j\in\mathbb N$
Množina všech planet P se tak rozpadne na několik neprázdných po dvou navzájem disjunktních podmnožin 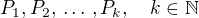$P_1,P_2,\,\ldots\,,P_k,\quad k\in \mathbb N$ .

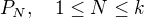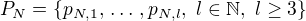Je zřejmé, že všechny tyto množiny mají alespoň 2 prvky. Předpokládejme, že některá z těchto množin obsahuje alespoň tři prvky, označme ji $P_N,\quad 1\leq N\leq k$ . Pak $P_N=\{p_{N,1},\,\ldots\,,p_{N,l},\ l\in\mathbb{N},\ l\geq 3\}$ . Na základě algoritmu, kterým byly planety očíslovány, platí, že astronom z planety 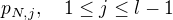$p_{N,j},\quad 1\leq j\leq l-1$ pozoruje planetu 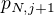$p_{N,j+1}$ . Otázkou je, kdo pozoruje planetu 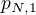$p_{N,1}$ . Astronom z planety 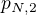$p_{N,2}$ to být nemůže, ten pozoruje planetu 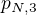$p_{N,3}$ . Stejně tak astronom planety $p_{N,j},\ j<l$ . Ten pozoruje planetu $p_{N,j+1}$ . 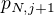Zbývá tedy astronom $p_{N,l}$ .

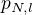Symbolem 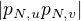$|p_{N,u}p_{N,v}|$ označme vzdálenost planet 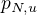$p_{N,u}$ a $p_{N,v}$ , $1\leq u,v\leq l,\ u\neq v$ .

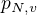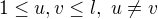Nechť tedy astronom planety 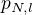$p_{N,l}$ pozoruje planetu 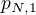$p_{N,1}$ . Pak nutně musí platit, že $|p_{N,1}p_{N,l}|<|p_{N,l}p_{N,l-1}|$ , jinak by astronom planety 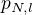$p_{N,l}$ pozoroval planetu 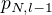$p_{N,l-1}$ . Stejně tak musí platit, že $|p_{N,l}p_{N,l-1}|<|p_{N,l-1}p_{N,l-2}|$ , jinak by planety 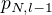$p_{N,l-1}$ pozoroval planetu 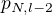$p_{N,l-2}$ , a to nelze. Stejným způsobem se ukáže, že $|p_{N,j+1}p_{N,j}|<|p_{N,j}p_{N,j-1}|,\ 2\leq j\leq l-1$ .

Dáme-li dohoromady všechny tyto nerovnosti, zjistíme, že

$|p_{N,1}p_{N,l}|<|p_{N,l}p_{N,l-1}|<|p_{N,l-1}p_{N,l-2}<|p_{N,l-2}p_{N,l-3}|<\dots<|p_{N,2}p_{N,1}|$

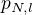A tedy $|p_{N,1}p_{N,l}|<|p_{N,2}p_{N,1}|$ , z čehož vyplývá, že planeta $p_{N,l}$ je planetě 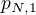$p_{N,1}$ blíže, než planeta 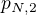$p_{N,2}$ . Což je spor s tím, že astronom planety 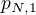$p_{N,1}$ pozoruje planetu 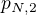$p_{N,2}$ . Tudíž předpoklad, že množina 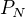$P_N$ má alespoň tři prvky, je chybný. Všechny množiny 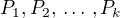$P_1,P_2,\,\ldots\,,P_k$ mají právě dva prvky. Ale protože tyto množiny jsou po dvou navzájem disjunktní a jejich sjednocením dostaneme množinu všech planet, musí tato množina obsahovat sudý počet prvků.

Matematické Fórum

#1 14. 12. 2008 15:55

matematický důkaz

#2 14. 12. 2008 16:58

Re: matematický důkaz

#3 14. 12. 2008 18:33 — Editoval Pavel (14. 12. 2008 19:24)

Re: matematický důkaz

Zápatí