Matematické Fórum

Polopat

Zdravím,

prosím o pomoc, v příkladu mám určit vzor množiny polynomů v určitém zobrazení, ale nevím, jak obecně zapsat polynom z té množiny (pomocí jakých koeficientů), abych pak už zbytek zvládl. Jedná se o množinu $\{x\in P_{3}|(\forall t\in <0, 1>)(x(t)=x(1-t))\}$ , kde $P_{3}$ je prostor polynomů stupně nejvýše 2 s přidáním nulového polynomu.

Zapsal jsem si obecně polynom a položil x(t)=x(1-t), vyjádřil t (s tím, že při dělení rovnice vyvstala potřeba řešit jeden případ zvlášť) a pak se mi chtělo řešit dvě nerovnice, jenže koeficienty u polynomů jsou komplexní (asi?) a komplexní čísla nejde uspořádat, takže jsem ve slepé uličce...

Andrejka3 · 03. 02. 2013 16:08

↑ Polopat:
Ahoj, možná by pomohlo, kdybys napsal, co Ti vyšlo.

Polopat · 03. 02. 2013 16:51

↑ Andrejka3:
Tak napsal jsem si 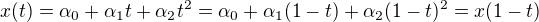$x(t)=\alpha _{0}+\alpha _{1}t+\alpha_{2}t^{2}=\alpha _{0}+\alpha _{1}(1-t)+\alpha_{2}(1-t)^{2}=x(1-t)$ a to jsem upravil.... a teď koukám, že jsem nezvlád převedení z jedné strany rovnice na druhou (trapas). No každopádně teď vyšlo 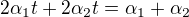$2\alpha_{1}t+2\alpha _{2}t=\alpha _{1}+\alpha _{2}$ . A teď teda nevím, jak to interpretovat. Chtěl bych najít ta alfa, že rovnice bude mít řešení pro všechna t z intervalu <0,1>, jenže když vyjádřím třeba $\alpha_{1}$ , tak to vyjádření bude platit jenom pro t různé od 1/2, takže to nechci. Ale jak jinak získám pro alfa nějakou podmínku?

Andrejka3 · 03. 02. 2013 17:26

↑ Polopat:
Ahoj, v této části matematiky trochu plavu. Myslím si, že pokud rovnost 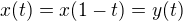$x(t)=x(1-t)=y(t)$ platí pro nekonečně mnoho $t$ (snad ale stačí i tři), že by měla platit ta rovnost všude, pro všechna t.
Pak by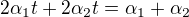
$2\alpha_{1}t+2\alpha _{2}t=\alpha _{1}+\alpha _{2}$
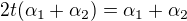$2t(\alpha_1 + \alpha_2)=\alpha_1+\alpha_2$ , tedy
$(\alpha_1 +\alpha_2)(2t-1)=0$ .
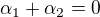Tedy $\alpha_1+\alpha_2 =0$ . Ale jistá si nejsem.

Polopat

↑ Andrejka3:
Aha, takže jestli to dobře chápu, tak ta podmínka, kterou hledám je teda 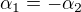$\alpha_{1}=-\alpha_{2}$ , přičemž na tom, jestli je v zadání t z <0,1> nebo třeba t z <1/4, 3/4>, vlastně až tolik nezáleží?

Andrejka3 · 03. 02. 2013 18:39

↑ Polopat:
Ano, to si myslim.

Polopat · 03. 02. 2013 18:49

↑ Andrejka3:
Super, děkuju.

Matematické Fórum

#1 02. 02. 2013 12:38 — Editoval Polopat (02. 02. 2013 21:36)

Množina polynomů

#2 03. 02. 2013 16:08

Re: Množina polynomů

#3 03. 02. 2013 16:51

Re: Množina polynomů

#4 03. 02. 2013 17:26

Re: Množina polynomů

#5 03. 02. 2013 18:29 — Editoval Polopat (03. 02. 2013 18:29)

Re: Množina polynomů

#6 03. 02. 2013 18:39

Re: Množina polynomů

#7 03. 02. 2013 18:49

Re: Množina polynomů

Zápatí