Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#6 05. 02. 2013 15:33 — Editoval honyik (05. 02. 2013 15:35)
Re: Limity
↑ Kittie:
Já nevím. Já jsem to taky nezaškrtával to "neexistuje", ale prostě ta stránka mi hlásí chybu, když to nezaškrtnu.
↑ dutahlava:
Tak si to představ: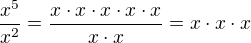
Vemeš jedno x z jmenovatele a vydělíš x z čitatele, což je 1.
Děkuji za pomoc! :)
Offline
#7 05. 02. 2013 18:03
Re: Limity
↑ dutahlava:
Ve skutečnosti se čitatel i jmenovatel vydělily  , protože je to nejvyšší mocnina x, kterou najdeme ve jmenovateli ;)
, protože je to nejvyšší mocnina x, kterou najdeme ve jmenovateli ;)
Přičemž si musíš uvědomit, že 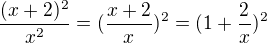
Offline

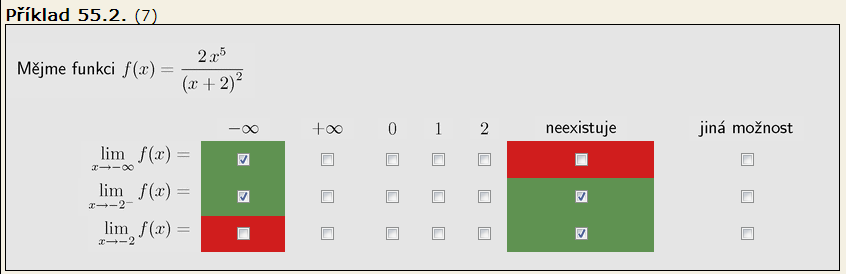

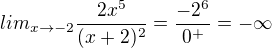 pro -2 zprava i zleva
pro -2 zprava i zleva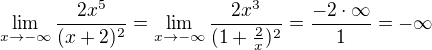
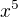 na
na  ? proc o 2?
? proc o 2?