Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 05. 02. 2013 00:34
Re: Spojitosti v R
Ahoj,
no jednoduše. Podíváš se, jak je definovaná spojitost :)
A zjistíš, že např.: a
a 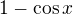 jsou spojité funkce (třeba z grafu), pak tě zajímá, co dělají v okolí bodu 0, kde (podle zadání) přecházejí jedna ve druhou, tzn. vypočítáš jednostrannou limitu tam, kde nemáš rovnítko a porovnáš s hodnotou v bodě, kde máš rovnítko.
jsou spojité funkce (třeba z grafu), pak tě zajímá, co dělají v okolí bodu 0, kde (podle zadání) přecházejí jedna ve druhou, tzn. vypočítáš jednostrannou limitu tam, kde nemáš rovnítko a porovnáš s hodnotou v bodě, kde máš rovnítko.
Offline
#5 05. 02. 2013 17:57
Re: Spojitosti v R
↑ honyik:
Tomu moc nerozumím.
Máš, zjistit, jestli je f(x) spojitá.
f(x) je definovaná pomocí funkce 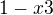 na intervalu
na intervalu 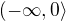
a pomocí funkce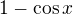 na intervalu
na intervalu 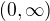
Tyto dvě funkce jsou samy o sobě všude spojité, tedy jediná nespojitost f(x) může být v bodě nula, kde je f(x) definovaná z každé strany jinak.
Dál viz můj předchozí příspěvek.
Offline



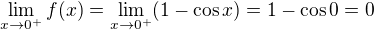
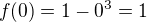
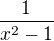 , x různé od 0
, x různé od 0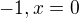
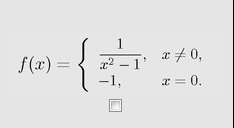
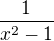 nen9 spojit8 v bodech -1 a 1, takže ani funkce f(x) nemůže být spojitá, i kdyby se v bodě 0 stavěla na hlavu. V 0 mimochodem spojitá je.
nen9 spojit8 v bodech -1 a 1, takže ani funkce f(x) nemůže být spojitá, i kdyby se v bodě 0 stavěla na hlavu. V 0 mimochodem spojitá je.