Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 02. 2013 21:47
Určitý integrál
Zdravím,
existuje nějaký rychlý způsob, jak zjistit, jestli je integrál kladný či záporný?
Protože třeba u druhé možnosti bych to dělal přes per partes, což je podle mě na dlouho.
Děkuji za pomoc! :)
Offline
- (téma jako vyřešené označil(a) honyik)
#4 05. 02. 2013 22:50
Re: Určitý integrál
honyik napsal(a):
Pochopil jsem to tak, že když mám kladné hodnoty v horní a dolní mezi, tak je integrál kladný.
Nie. Pri ulohach tohoto typu je dobre vediet si aspon priblizne predstavit graf funkcie pod integralom. A pamatat na to, ze plocha pod osou x sa berie so zapornym znamienkom, nad osou x s kladnym. Teda integral nezapornej funkcie je nezaporny bez ohladu na hranice, samozrejme predpokladam, ze dolna hranica je mensia ako horna.
Offline
#5 05. 02. 2013 23:11
Offline

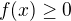 na intervalu I, potom
na intervalu I, potom 
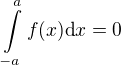 , je-li f(x) lichá funkce. Toto můžeš využít u druhého a třetího příkladu.
, je-li f(x) lichá funkce. Toto můžeš využít u druhého a třetího příkladu.