Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Pevný bod permutace (TOTO TÉMA JE VYŘEŠENÉ)
#1 05. 02. 2013 20:38
Pevný bod permutace
Ahoj, mohli byste mi prosím pomoci?
Řeším problém: "Kolik je permutací n prvků s právě jedním pevným bodem?"
Moje úvaha je taková, že pokud mám jeden pevný bod zbylé prvky mohu zpermutovat (n-1)! a právě ten jeden bod mohu umístit n způsoby tedy výsledek je --> n*(n-1)! = n!. Je to takto správně?
Co kdyby by byli dva pevné body?
Offline
- (téma jako vyřešené označil(a) Optix)
#3 05. 02. 2013 20:58
Re: Pevný bod permutace
Tak teď nevím jestli jsi mi tímhle chtěl dát najevo jako že je moje úvaha správná nebo ne, protože jsem se akorát utvrdil v tom že jsem uvažoval správně, tak jestli to byl záměr tak děkuju :)
Spíše mi vrtá hlavou ty dva pevné body ...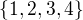 mějme tedy tyto prvky pokud chci utvořit permutaci s 2 pevnými, pak mám navýběr (n-2)! ale pak dál nevím, nemohl bys mě trochu pošťouchnout a nasměrovat?? :)
mějme tedy tyto prvky pokud chci utvořit permutaci s 2 pevnými, pak mám navýběr (n-2)! ale pak dál nevím, nemohl bys mě trochu pošťouchnout a nasměrovat?? :)
Offline
#4 05. 02. 2013 21:12
Re: Pevný bod permutace
Úplně z cesty neuvažuješ, ale všechno sis neohlídal. A nějak jsem doufal, že když si vypíšeš všechny permutace 3 (nebo 4) prvků a poctivě spočítáš pevné body, tak to bude snazší než nějaké vysvětlování. V té své úvaze totiž zafixuješ 1 bod, ale už nehlídáš, aby se další pevný bod neobjevil v té permutaci zbytku.
Offline
#5 05. 02. 2013 21:20
Re: Pevný bod permutace
A jo děkuju až teď když jsi mi to napsal naprosto po lopatě, jsem si všimnul že já sám jsem tam napsal právě jeden, to mi tu úlohu značně zkomplikovalo, teď mi tedy vyšel poloviční počet, ale stále nevím jak přijít na nějaký obecný vzorec, tedy jestli existuje.. neboť mi třeba u 4 prvkové a dvou pevných bodů vyšla pouze jedna permutace což se mi moc nezdá :((
Offline
#6 05. 02. 2013 23:04
Re: Pevný bod permutace
Vidím, že téma je už vyřešené, ale přihodím svůj výtvor. Jednak pro kompletnost a druhak tím třeba vyprovokuju někoho, kdo mi napíše, že se v tom hrabu hrozně neobratně a přidá nějaké úžasné a jednoduché řešení, které ta úloha třeba má.
Koment k předchozímu vývoji tématu:
K problému. Můj aktuální pocit je, že řešení půjde naindukovat.
Vydělíme si z našich prvků jeden červený, n-tý. Libovolnou permutaci n prvků lze jednoznačně vyjádřit tak, že zpermutujeme n-1 prvků a n-tý buď necháme na místě, nebo ho v závěru prohodíme s některým z prvních n-1 prvků.
Zřejmě {počet permutací n prvků s 1 p.b.} = n*{počet permutací n-1 prvků s 0 p.b.}.
A počet permutací s 0 p.b. si naindukujeme:
Z řešení této jednoduché rekurence už prakticky vypadne výsledek. Je jasné, že nějaká taková rekurence by se vymyslela i pro libovolných k pevných bodů.
Pak mě taky napadá, že pro obecných k p.b. by možná byla snazší cesta přes úvahu, že každá permutace jde (až na nějaké pořadí) jednoznačně rozložit na disjunktní cykly. Pokud by to bylo průchozí, tak by se tam asi lépe postihnul koncept "právě k pevných bodů". Ale nevím. Jen nápad. Já se do toho určitě pouštět nebudu.
Offline
#7 06. 02. 2013 12:36
Re: Pevný bod permutace
Ahoj ↑ anes:,
Len male doplnkove citanie
http://mathworld.wolfram.com/Derangement.html
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Pevný bod permutace (TOTO TÉMA JE VYŘEŠENÉ)

 .
. byl počet permutací s aspoň 1 pevným bodem (na první pohled; vždyť všech permutací je
byl počet permutací s aspoň 1 pevným bodem (na první pohled; vždyť všech permutací je  , ale přiznávám, že mi to taky dochází až teď). Potíž je v tom, že permutaci, která má
, ale přiznávám, že mi to taky dochází až teď). Potíž je v tom, že permutaci, která má  pevných bodů, máš v tom čísle započtenou k-krát.
pevných bodů, máš v tom čísle započtenou k-krát.