Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 06. 02. 2013 23:40
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Graf - derivace v bodě
↑ honyik: To sú tie body, v ktorých je funkcia rýdzo rastúca.
Offline
#3 07. 02. 2013 08:57
#4 07. 02. 2013 09:04 — Editoval Creatives (07. 02. 2013 09:20)
Re: Graf - derivace v bodě
Jinak receno:
Derivace funkce v bode je smernice tecny(smernice je tangens uhlu) takze je treba si uvedomit jak vypada funkce tan. A potom jestli sestrojis tecnu v bode, ktera bude svirat s osou x uhel vetsi nez 0 az do 90 tak derivace bude kladna, jestli bude svirat 90-180 tak bude zaporna. Pekne to jde videt na fci x^2. Jestli bude tecna rovnobezna tak derivace je v tomto bode rovna 0.
Offline
#5 07. 02. 2013 09:13 — Editoval Creatives (07. 02. 2013 09:20)
Re: Graf - derivace v bodě
↑ Bati:
To nevis??pokud existuje nejake redukované okoli bodu ktere je podmnozinou Df. Tak pro leve jeho okoli je fx mensi nez v tom bode a pro prave okoli je funkcni hodnota mensi nez fx.
Offline
#6 07. 02. 2013 09:31 — Editoval Bati (07. 02. 2013 09:32)
Re: Graf - derivace v bodě
↑ Creatives:
Já to vím, ale, chtěl jsem, aby to bylo vysvětleno tazateli, protože je to v tomhle příkladu velmi důležité.
Navíc sám jsi to vysvětlil špatně: Oba zapomínáte na spojitost - tvé definci např. vyhovuje fce signum v bodě nula, i když tam nemá derivaci.
Offline
#8 07. 02. 2013 13:00
Re: Graf - derivace v bodě
Koukám - příspěvků plno a vysvětlení téměř žádné. Takže - derivace funkce f(x) v bodě x_0 je limita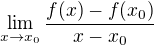
pokud tato limita existuje. K tomu, aby taková derivace existovala, musí být především funkce definována v bodě x_0. Je tedy okamžitě jasné, že v x_0 neexistuje derivace ve druhém případě (funkce nemá v x_0 funkční hodnotu).
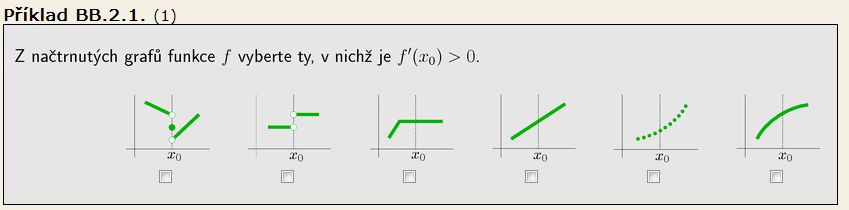
Dále je nutné, aby funkce byla spojitá na jistém okolí bodu x_0 (s eventuální výjimkou bodu x_0). Z tohoto důvodu nemá derivaci funkce na pátém obrázku.
Dále je důležité, zda je derivace definována jako limita vlastní, anebo se připouští i limita nevlastní (což se někdy připouští). Pokud bychom připustili i nevlastní limitu jako derivaci, pak by taková derivace existovala i v prvním případě (byla by minus nekonečno). Většinou se však derivace definuje jako limita vlastní. Pak je to (geometricky) směrnice tečny ke grafu funkce. Taková derivace tedy v prvním případě neexistuje. Vlastní derivace tedy existuje jen v případech 3, 4, 6, přičemž v případě 3 je rovna nule, takže nevyhovuje zadání. V případech 4 a 6 je f'>0, takže jsou OK.
Pokud jde o jednostranné derivace, jsou to jednostranné limity, v ostatním platí vše, co bylo řečeno výše. První případ je má, pokud připustíme derivace nevlastní (obě jsou mínus nekonečno), anebo je nemá, je-li derivace definována pouze jako limita vlastní. Druhý případ je nemá (chybí funkční hodnota v x_0). Pátý případ je nemá, protože není spojitý na žádném okolí. Zbylé případy je mají, ve všech jsou jednostranné derivace rovny derivaci "oboustranné", třetí případ nevyhovuje - derivace jsou rovny nule.
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline

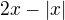 je rostoucí v každém bodě, přičemž v 0 nemá derivaci.
je rostoucí v každém bodě, přičemž v 0 nemá derivaci.