Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 02. 2013 10:44
příklad s grupou
Dobrý den. Potřebuji poradit, jak korektně dokázat toto tvrzení: Dokažte, že v konečné grupě sudého(lichého) řádu je počet prvků řádu 2 lichý(sudý). Díky.
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
- (téma jako vyřešené označil(a) Honza90)
#2 10. 02. 2013 13:17
Re: příklad s grupou
Uvažoval bych asi takto:
Řád konečné grupy je počet jejich prvků. Ke každému prvku musí existovat inverzní. Prvek a je řádu dvě právě tehdy, když a^2=e, tj. když je sám sobě prvkem invezním, tj. grupa může mít libovolný počet prvků 2. řádu. Prvek lichého řádu není k sobě inverzní, musí "generuje" dva různé prvky lichého řádu – sám sebe + svoji inverzi. Neutrální prvek je vždy řádu jedna (tj. lichého)...
A pokud bych to chtěl mít zcela dogmaticky, asi bych na to šel indukcí:
n=1: Triviální grupa je řádu jedna a má jeden prvek lichého řádu a nula prvků sudého. Věta platí...
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#3 10. 02. 2013 13:19 — Editoval Andrejka3 (10. 02. 2013 13:24)
Re: příklad s grupou
Počet prvků řádu 1 je kolik?
Proveďme rozklad grupy na třídy podle řádu prvku: třeba R_n označme všechny prvky grupy řádu n (pro taková n, aby R_n byla neprazdna).
n=2: kazdy prvek řádu dva generuje dvouprvkovou podgrupu, ve které je ten prvek sám (je svou inverzí) a neutrální prvek.
n>2: na G_n je operace inverze bijekcí G_n do G_n, tedy permutaci. Nemuze mit tato permutace pevny bod (proc?). Kazdy cyklus teto permutace ma delku ... (ted nevim, jak se presne definuje delka cyklu permutace, ale chci rict, ze inverze inverze je identita).
Takze G_n muzes rozlozit na cykly delky dva. Je tedy |G_n| sude.
Edit: Tak jsme se tu hezky sešli. Zdravím ↑ martisek:, ↑ Brano:.
What does a drowning number theorist say?
'log log log log ...'
Offline

 má rád
má rád  potom aj
potom aj 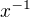 má rád
má rád  tak
tak  alebo
alebo  .
. je párny počet a teda prvkov s rádom
je párny počet a teda prvkov s rádom