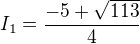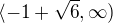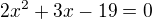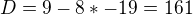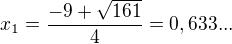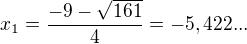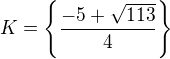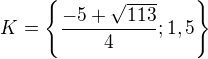Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 02. 2013 14:04
Rovnice s neznámou v absolutní hodnotě
Dobrý den, jsem zde nový, tak nevím, jestli se správně dotazuji. Mám problém s touto úlohou :
Řešte v R rovnice :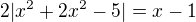
Když chci vyřešit D z kvadratické rovnice vyjde mi 24. A tady nevím jak dál postupovat, aby mě vyšlo x1 a x2. Poté si je dám jako intervaly a řeším normálně, jako kdyby tam ta kvadratická rovnice nebyla.
Děkuji
Offline
#2 10. 02. 2013 14:08 — Editoval Polopat (10. 02. 2013 14:11)
Re: Rovnice s neznámou v absolutní hodnotě
↑ eda220:Ahoj,
kořeny získáš jako u každé kvadratické rovnice ze vzorce 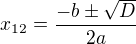 . Dál by sis rozdělil
. Dál by sis rozdělil  na intervaly a podle toho odstraňoval absolutní hodnotu.
na intervaly a podle toho odstraňoval absolutní hodnotu.
P.S. Předpokládám, že v zápise je chyba a má bát druhý člen v abs. hodnotě na prvou.
Offline
#4 10. 02. 2013 14:13
Re: Rovnice s neznámou v absolutní hodnotě
↑ eda220:
24 se dá rozložit a to se potom dá částečně odmocnit. Jinak nějaká odmocnina tam v tomhle případě zůstane a nezbavíme se jí a prostě ji budeme muset pořád psát, ale je to lepší, než ťuknout do kalkulačky a zaokrouhlit.
Věděl bys, jak 24 rozložit a to pak částečně odmocnit?
Offline
#9 10. 02. 2013 14:49
Re: Rovnice s neznámou v absolutní hodnotě
Děkuji, to jsem pochopil. Teď ovšem jak řeším na číslené ose, tak nevím jiě jestli vycháí :
Mám tedy :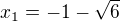
a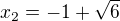
Nejprve řeším a) 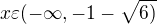
Což bude : 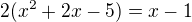
Upravím :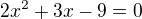
Počítám 
tedy : 
Vyjde mi : 
A teď jak dál ? (tedy jestli mám správně výsledek), Děkuji.
Offline
#10 10. 02. 2013 15:01 — Editoval Polopat (10. 02. 2013 15:11)
Re: Rovnice s neznámou v absolutní hodnotě
↑ eda220:
Zapomněl jsi na  .
. 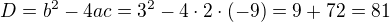 , tedy
, tedy 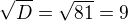 . Vyjdou ti dva kořeny a ty musíš zkontrolovat, jestli leží v intervalu, pro který to teď počítáme. Tady se přiznám, že jsem musel použít kalkulačku, protože odhady odmocnin mi nikdy moc nešly.
. Vyjdou ti dva kořeny a ty musíš zkontrolovat, jestli leží v intervalu, pro který to teď počítáme. Tady se přiznám, že jsem musel použít kalkulačku, protože odhady odmocnin mi nikdy moc nešly.
Možná bude vědět někdo jiný tady?
Offline
#20 10. 02. 2013 16:31
Re: Rovnice s neznámou v absolutní hodnotě
Už sem na to přišel, dvě chyby : jednak hned a začátku v úpravě a potom v dosazení do vzorce pro výpočet kořenů.
Zaráží mě tedy výsledek 1.intervalu, který je 1,5. Ale kořen rovnice je jen 
Offline
#21 10. 02. 2013 16:41 — Editoval Polopat (10. 02. 2013 17:01)
Re: Rovnice s neznámou v absolutní hodnotě
↑ eda220:
V prvním intervalu jsme našli dva kořeny rovnice bez abs. hodnoty, ale žádný neleží v tom intervalu, takže pro první interval nemáme žádné řešení rovnice s abs. hodnotou. Pro druhý interval jsme také našli dva kořeny, ale jenom jeden je řešením, protože leží v daném intervalu. Pro třetí interval jsme našli také dva kořeny (stejné jako pro první) a řešením rovnice je jeden z nich a sice 1,5, protože leží v intervalu 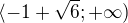 .
.
Offline

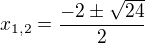

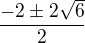
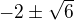
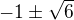 .
.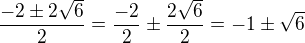 .
.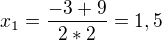
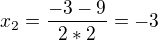
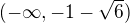 , protože
, protože 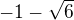 je -3,449... Tak, zkusím počítat dál, ještě ve dvou intervalech. Tohle asi mám správně ?
je -3,449... Tak, zkusím počítat dál, ještě ve dvou intervalech. Tohle asi mám správně ?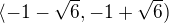

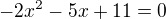
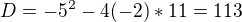
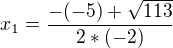
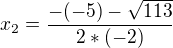
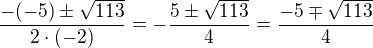 .
.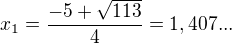

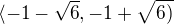 je jen x1, takže
je jen x1, takže