Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1

 

#1 10. 02. 2013 22:06

mp3jj
Příspěvky: 419
Pozice: student
Reputace:   5 
 

Vennovy diagramy

Dobrý den,

nemohu se u tohoto příkladu pohnout správným směrem.
Zadání:
http://forum.matweb.cz/upload3/img/2013-02/29967_34.gif

Podle schématu jsem sestavil rovnice:
http://forum.matweb.cz/upload3/img/2013-02/30343_nacrt.jpg

a+b+c+d+e+f+g+h=28
a+b+d+e=14
b+d+c+f=12
d+e+f+g=10
h=6
d=4
b+e+f=?

Jediný, co mě napadlo, bylo dosadit "h" a "d" a trochu to zjednodušit. Potom v tom ale nevidím nic, co by se dalo nějak sečíst /odečíst.

a+b+c+e+f+g=18
a+b+e=10
b+c+f=8
e+f+g=6

b+e+f=?

Offline

  • (téma jako vyřešené označil(a) mp3jj)

#2 10. 02. 2013 22:11

Blackflower
Místo: Bratislava
Příspěvky: 1303
Škola: FMFI UK BA, EFM, absolvent 2016
Pozice: aktuár
Reputace:   71 
 

Re: Vennovy diagramy

↑ mp3jj: Len taký nápad... nebolo by lepšie použiť vzťahy $|A\cup B|=|A|+|B|-|A\cap B|$ a pod.? (Neviem teda, či to správne zapisujem, ale vieš, čo myslím?)

https://www.facebook.com/MatematickeVtipy

Offline

 

#3 10. 02. 2013 22:23

mp3jj
Příspěvky: 419
Pozice: student
Reputace:   5 
 

Re: Vennovy diagramy

↑ Blackflower:
My vždycky vennovy diagramy zapisovali tak, jak jsem začal. :-) To, co jsi napsala je určitě pravda, ale tím, jak tam jsou 3 množiny, tak nevím, jak by se to dalo vhodně nakombinovat. Protože i v průniku A a B máš část C. Možná to myslíš dobře, ale v tuto chvíli mi pořád nedochází, jak by mi to mohlo pomoci :(

↑ martisek:
...má to vyjít 6 žáků....

Offline

 

#4 10. 02. 2013 22:39

mp3jj
Příspěvky: 419
Pozice: student
Reputace:   5 
 

Re: Vennovy diagramy

Teď jsem zkusil toto:

I) a+b+c+e+f+g=18
a+b+e=10.... a=10-b-e
b+c+f=8...... c=8-b-f
e+f+g=6..... g=6-e-f

když dosadím a,c,g do rovnice I), upraví se to na -e-b-f=-4, z toho tedy hledané e+b+f=4. Ale má to vyjít 6. :(

Offline

 

#5 10. 02. 2013 22:42

mp3jj
Příspěvky: 419
Pozice: student
Reputace:   5 
 

Re: Vennovy diagramy

mp3jj napsal(a):

Teď jsem zkusil toto:

I) a+b+c+e+f+g=18
a+b+e=10.... a=10-b-e
b+c+f=8...... c=8-b-f
e+f+g=6..... g=6-e-f

když dosadím a,c,g do rovnice I), upraví se to na -e-b-f=-4, z toho tedy hledané e+b+f=4. Ale má to vyjít 6. :(

Chyba výpočtu, vyjde to nakonec -e-b-f=-6, takže 6. :D

Přesto děkuju všem za snahu a ochotu. :)

Offline

 

#6 10. 02. 2013 22:42

Arabela
Příspěvky: 1927
Reputace:   181 
Web
 

Re: Vennovy diagramy

Ahoj ↑ mp3jj:,
ja som sa pokúsila zostaviť sústavu rovníc s menším počtom neznámych, a to tak, že čo bolo dané konkrétne, zapísala som priamo do Vennovho diagramu. Aby sme sa lepšie rozumeli, ostatné Tvoje označenia som ponechala - takže namiesto d máme 4 a namiesto h máme 6.
Pýtajú sa na súčet b+e+f, označme si ho ako x.
Máme túto sústavu rovníc:
a+b+e+4=14
b+c+f+4=12
e+f+g+4=10
a+b+c+e+f+g+4+6=28.

Sčítajme ľavé a pravé strany prvých troch rovníc:
a+2b+c+2e+2f+g+12=12+10+14,
a keď použijeme b+e+f=x,
dostávame z toho 2x+a+c+g=24.

Z poslednej štvrtej rovnice po substitúcii b+e+f=x dostaneme
                           x+a+c+g=18.
Keď vyjadríme a+c+g z oboch posledných rovníc a porovnáme, dostaneme
24-2x=18-x,
x=6.
Skúškou sa presvedčíme, že všetko sedí...

server.gphmi.sk/~domanyov

Offline

 

#7 10. 02. 2013 22:46

mp3jj
Příspěvky: 419
Pozice: student
Reputace:   5 
 

Re: Vennovy diagramy

↑ Arabela:

Děkuju za víc možností řešení, výsledek také vychází správně. :)

Offline

 

#8 10. 02. 2013 22:58 — Editoval Arabela (10. 02. 2013 23:23)

Arabela
Příspěvky: 1927
Reputace:   181 
Web
 

Re: Vennovy diagramy

Ahoj ↑ Blackflower:,
ono by to šlo aj podľa Tvojho návodu - len by bolo treba použiť vzorec pre tri množiny:
$|A\cup B\cup C|=|A|+|B|+|C|- $
$-|A\cap B|-|A\cap C|-|B\cap C|+ $
$+|A\cap B\cap C| $

Podľa toho by platilo:
28-6 = 14+12+10-(b+4) - (e+4) - (f+4) +4,
odtiaľ
b+e+f = 40-12-22 = 6

server.gphmi.sk/~domanyov

Offline

 

#9 10. 02. 2013 23:00

Arabela
Příspěvky: 1927
Reputace:   181 
Web
 

Re: Vennovy diagramy

↑ mp3jj:,
nedalo mi, a zareagovala som aj na myšlienku Blackflower. S použitím toho vzorca je výpočet samozrejme o dosť kratší...

server.gphmi.sk/~domanyov

Offline

 

#10 10. 02. 2013 23:24

mp3jj
Příspěvky: 419
Pozice: student
Reputace:   5 
 

Re: Vennovy diagramy

↑ Arabela:
Jo, tak to vypada, ze ten priklad byl delanej primo na tento vzorecek. Bylo to ted ve scio testech z matiky, to ale nemuzou pocitat s tim, ze si tento vzorecek nekdo pamatuje.....:(

Offline

 

#11 10. 02. 2013 23:26

Blackflower
Místo: Bratislava
Příspěvky: 1303
Škola: FMFI UK BA, EFM, absolvent 2016
Pozice: aktuár
Reputace:   71 
 

Re: Vennovy diagramy

↑ Arabela: Mne napadlo, že či by sa nedali zobrať zakaždým dve množiny (3 dvojice), ale takto je to určite jednoduchšie a asi aj správnejšie. :)

https://www.facebook.com/MatematickeVtipy

Offline

 

#12 10. 02. 2013 23:26

Arabela
Příspěvky: 1927
Reputace:   181 
Web
 

Re: Vennovy diagramy

↑ mp3jj:,
áno, počítať s tým, že si tento vzorec niekto bude pamätať, je naozaj dosť "drsné"...

server.gphmi.sk/~domanyov

Offline

 

#13 10. 02. 2013 23:28 — Editoval Blackflower (10. 02. 2013 23:29)

Blackflower
Místo: Bratislava
Příspěvky: 1303
Škola: FMFI UK BA, EFM, absolvent 2016
Pozice: aktuár
Reputace:   71 
 

Re: Vennovy diagramy

↑ mp3jj: To sa dá aj odvodiť, aj keď netvrdím, že je to triviálne... napríklad si zoberme dve množiny. Keď chceme spočítať počet ich prvkov, spočítame počet prvkov jednej a druhej, no zarátali sme dvakrát to, čo majú spoločné. Takže raz to musíme odrátať.
Pri trochu množinách postupujeme podobne - spočítame počet prvkov všetkých množín zvlášť. Dvakrát sme zarátali prieniky dvojíc, takže ich raz musíme odrátať. No teraz sme však odrátali príliš veľa krát prienik všetkých troch, takže ho treba prirátať.
(Snáď je to aspoň trochu zrozumiteľné...)

https://www.facebook.com/MatematickeVtipy

Offline

 

#14 10. 02. 2013 23:30

Arabela
Příspěvky: 1927
Reputace:   181 
Web
 

Re: Vennovy diagramy

↑ Blackflower:,
pekne si to vysvetlila...:)

server.gphmi.sk/~domanyov

Offline

 

#15 10. 02. 2013 23:49 — Editoval mp3jj (10. 02. 2013 23:51)

mp3jj
Příspěvky: 419
Pozice: student
Reputace:   5 
 

Re: Vennovy diagramy

↑ Blackflower:
Opravdu pekny vysvetleni a jednoduse receno :). Chtel jsem se zeptat, proc je na konci vzorecku plus u pruniku vsech tri mnozin, ale pak jsem si rek, ze to asi nebudu pitvat, ze by to bylo na dlouhou analyzu :D....kdyz uz jsi tedy zacala a jsme teda v te debate; porad mi vrta hlavou: prunik tri mnozin odecitam trikrat, jako soucast pruniku dvou mnozin, ale prictu to tedy nakonec jen jednou? To mi prijde takovy zvlastni :)

...jestli to je na nejaky velky rozbor, tak to nechte, jen me to tak napadlo...

Offline

 

#16 11. 02. 2013 00:32 — Editoval Blackflower (11. 02. 2013 00:33)

Blackflower
Místo: Bratislava
Příspěvky: 1303
Škola: FMFI UK BA, EFM, absolvent 2016
Pozice: aktuár
Reputace:   71 
 

Re: Vennovy diagramy

↑ mp3jj: Už som aj chcela ísť spať, ale nedá mi to :D ponúkam nejaký náčrt dôkazu, ale neviem, či by mi ho nejaký pán učiteľ perfekcionista uznal.
Pomôžem si obrázkom: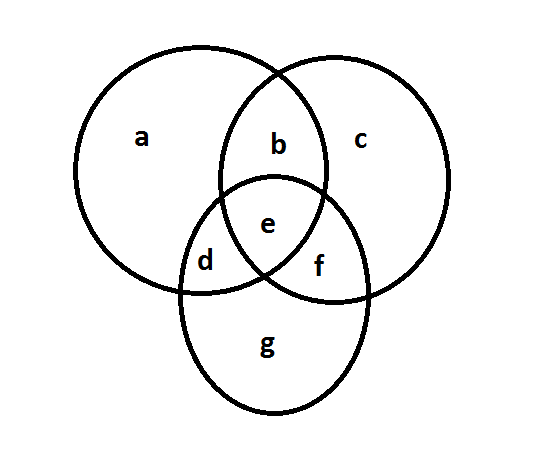
http://forum.matweb.cz/upload3/img/2013-02/38812_Untitled.png
Súčet prvkov množín je a+b+c+d+e+f+g. Idem na to postupne.
Najprv spočítam |A|+|B|+|C|=(a+b+d+e)+(b+c+e+f)+(d+e+f+g)=a+2b+c+2d+3e+2f+g. Potrebujem sa zbaviť jedného b, jedného d, jedného f a dvoch e.
|A|+|B|+|C|-(prieniky po dvoch)=a+2b+c+2d+3e+2f+g-(b+e)-(d+e)-(e+f)=a+b+c+d-0e+f+g
Tým to bude. Aj ja som na to prišla až počas písania svojej úvahy priamo sem...

https://www.facebook.com/MatematickeVtipy

Offline

 

#17 11. 02. 2013 08:35

Arabela
Příspěvky: 1927
Reputace:   181 
Web
 

Re: Vennovy diagramy

↑ Blackflower:,
super! Ja som večer rozmýšľala, že vytvorím obrázky Vennových diagramov  so šrafovaním (jednoduchým, dvojitým a trojitým), aby som dokázala rovnosť ľavej a pravej strany v tom vzorci. Bolo ale už neskoro večer, tak som šla spať. Dokonca mi napadol príklad s polopriesvitným farebným papierom, ktorý keď kladieme na seba, mení stupeň intenzity farby - cieľom by bolo vytvoriť iba jednu vrstvu, takže po úvodnom pokrytí každého z oválov jednou vrstvou a pri postupnom "vystrihovaní" vrstvy tam, kde sú dve, resp. tri, tam by bolo jasne vidieť, že poslednú z vrstiev by bolo možné odstrániť až po pridaní jednej vrstvy do prostriedku...
Ale Ty si to urobila jednoducho a názorne, hoci v podstate bez obrázku (len s tým úvodným). Pekné!

server.gphmi.sk/~domanyov

Offline

 

#18 11. 02. 2013 09:22

Blackflower
Místo: Bratislava
Příspěvky: 1303
Škola: FMFI UK BA, EFM, absolvent 2016
Pozice: aktuár
Reputace:   71 
 

Re: Vennovy diagramy

↑ Arabela: ďakujem :) pravdupovediac, mne vôbec nenapadlo, že to e úplne vypadne, robila som to úplne naslepo s tým, že snáď to vyjde :D

https://www.facebook.com/MatematickeVtipy

Offline

 

#19 11. 02. 2013 09:36

mp3jj
Příspěvky: 419
Pozice: student
Reputace:   5 
 

Re: Vennovy diagramy

Aháá...:) tak tes uz tomu rozumim uplne dokonale! ;) Opravdu moc dekuju, dobra prace! :D

Offline

 

 

Stránky: 1

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson