Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1

 

#1 18. 02. 2013 18:13 — Editoval Honza90 (18. 02. 2013 18:52)

Honza90
Příspěvky: 370
Reputace:   4 
 

metrický prostor - důkaz

Dobrý den. Poradil by mi někdo s tímhle důkazem. Mě se to takhle zdá až příliš jednoduché:

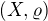Ukažte, že uzavřená podmnožina $A$ úplného mterického prostoru $(X,\varrho )$ je sama úplným metrickým prostorem.

Nechť $\{a_{n}\}_{n=1}^{\infty }$ je cauchyovská posloupnost v $A$, která zřejmě konverguje k $x\in X$. $A$ je uzavřená, takže obsahuje hromadné body všech svých posloupností. Potom tedy $x\in A$ a $(A,\varrho )$ je úplný metrický prostor.

Wir müssen wissen. Wir werden wissen. David Hilbert

Offline

  • (téma jako vyřešené označil(a) Honza90)

#2 18. 02. 2013 19:42

Brano
Příspěvky: 2655
Reputace:   231 
 

Re: metrický prostor - důkaz

Jednoduche, ale spravne :-)

Offline

 

 

Stránky: 1

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson