Matematické Fórum

liamlim

zdravím

tak sem si řekl, že bych rád trochu více porozuměl nerovnostem, a nejsem si jistý, jestli jsem dobře pochopil kdy je výraz homogenní a co vše z toho můžu vyvodit. Nevím, kde bych měl téma, které je v podstatě jen dotazem, přispět, ani nevím, jestli se něco takového na SŠ probírá. Dřív jsem ale přispíval do sekce SŠ a byl sem přesunutý, tak když by to sem nepatřilo, také prosim o přesunutí.

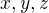takže jak homogenií výrazy chápu já: Třeba mějme nerovnost: $x^4y+y^4z+z^4x\ge x^2y^2z+y^2z^2x+x^2z^2y$ kterou máme pro kladná $x,y,z$ dokázat. To jde docela pěkně například pomoci AG, ale já zkusím něco jiného:

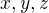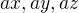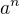já to, že je nerovnice homogenní určitého stupně chápu tak, že když místo $x,y,z$ dosadím $ax,ay,az$ kde $a$ je kladné, pak na obou stranách vytknu n-tou mocninu $a$ tak aby $n$ bylo co nejvyšší, pak po vydělení nerovnice číslem $a^n$ dostaneme opět původní nerovnici.

první otázka: chápu to dobře nebo jsem to pochopil úplně špatně?
druhá otázka: je tedy tato nerovnost homogenní stupně 5?
třetí otázka: $a$ můžu dosadit opravdu libovolné kladné číslo? Můžu si třeba říct, že $a$ bude takové kladné číslo, pro které $x=1$ , nebo $xyz=2$ nebo $xy^2+z^3=1$ ? teď mi nejde o užitečnost tohoto kroku ale jestli je to možné

pozn.: tu nerovnici dokázat umím, dal sem ji sem hlavně kvůli dotazu dva, jesti chápu dobře jak vypadá homogenní nerovnost.

Omlouvám se za tento dotaz, ale chtěl bych mít v něčem jasno, než můžu zase zkusit něco jiného. Není prti pravidlům když do stejného tématu vložím více dotazů v delším čase? teď asi nějaký čas budu řešit nerovnosti a nechce se mi zakládat pokaždé jiné téma. ani nevím kam tato témata patří.

Kondr · 20. 02. 2013 20:18

1) ano, chápeš to dobře
2) ano
3) položit f(x,y,z)=k lze jen tehdy, když pro každou trojici x,y,z existuje a takové, že f(ax, ay, az)=k. Např. pokud x,y,z mají být kladná,
můžeš položit x+y+z=1, pokud by mohla být i záporná, je pro takovou substituci potřeba ukázat, že nerovnost platí i v případě, kdy x+y+z=0. Pokud chceš položit x-y=1, je třeba rozebrat zvlášť případ x=y. A tak dál.

liamlim

zdravím všechny. pokračoval sem v nerovnostech, a už toho začínám mít dost. často se stane, že se někam dostanu, a pak nejsem schopný úlohu "dorazit". jako například teď když jsem našel někde na internetu pěknou nerovnost

$\frac{1}{a^3(b+c)}+\frac{1}{b^3(a+c)}+\frac{1}{c^3(a+b)}\ge\frac{3}{2}$ která se má dokázat pro všechna kladná a,b,c se součinem 1. Po delŠím trápení se se mi myslím podařilo dostat k nerovnici, $(k+1)^2+k(a+1)^2(a-2)\ge 0$ kterou mi podle všeho stačí dokázat, abych dokázal zmíněnou nerovnost. jenže tady sem skončil, jak mám podobnou nerovnost dokazovat? přes diskriminant? nebo nějak jinak? prosím o každou radu, děkuji.

pozn.: měl bych asi vysvětlit, kde se mi tam vzalo kladné $k$ . já sem první dokázal, že pro libovolná kladná a,c existují kladná x,y taková, že $a=\frac{x}{y}$ a $b=xy$ no a tak sem místo $a$ a $c$ dosadil do nerovnice $\frac{a}{k}$ a $ak$ kde $\frac{a}{x}\cdot b\cdot ak=1$ neboli $a^2b=1$ . po několika úpravách, a použiti cauchyho nerovnosti mi vyšla právě tato nerovnost. Dosazoval sem kladné hodnoty menší než 2 a vypadá to, že platí. - ale byl to jenom odhad, který jsem vytvořil, ale i tak mi stačí k dokázání zmíněné nerovnice

edit: omlouvám se, mám to asi blbě. stačí dosadit 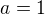$a=1$ a nerovnost nebude pro libovolné kladné $k$ platit. i tak se ale ptám, bylo mé dosazení správné? děkuji

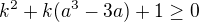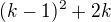edit2: myslím, že tady ještě to mám dobře: že nerovnost $k^2+k(a^3-3a)+1\ge 0$ skutečně platí. teď sem původně viděl člen $k^2$ a $1$ tak sem si řekl, že je to to samé co $(k+1)^2-2k$ ale když tak nad tím přemýšlím, klidně jsem mohl zvolit $(k-1)^2+2k$ a měl bych dokazovat nerovnost $(k-1)^2+k(a^3-3a+2)\ge0$

edit3: která ale platí! protože je vlastně stejná jako : $(k-1)^2+k(a-1)^2(a+2)\ge0$ což je součet dvou kladných členů. prosím, nezkusí někdo zopakovat můj postup, jestli sem nerovnici vyřešil správně? strávil sem nad tím dost času a to mé dosazení trojice a/k ; b ; ak - to si nejsem jistý jestli sem udělal správně. díky

Matematické Fórum

#1 18. 02. 2013 15:52 — Editoval liamlim (18. 02. 2013 15:53)

nerovnost

#2 20. 02. 2013 20:18

Re: nerovnost

#3 24. 02. 2013 12:53 — Editoval liamlim (24. 02. 2013 13:18)

Re: nerovnost

Zápatí