Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 18. 02. 2013 08:44
- JohnPeca18

- Příspěvky: 651
- Škola: MFF UK
- Pozice: Absolvent 2014
- Reputace: 81
k-algebra
ahoj,
chcel by som sa spýtať, neviete niekto, čo je to algebra nad polom? Teda Algebra over field. Niečo
som si hľadal ale nejak som to nepochopil. Konkrétne napríklad tu
http://www.math.harvard.edu/~elkies/M25 … gebra.html
Fix a (commutative) field k, which will be our ``base field''. An algebra over k, or more simply a k-algebra, is an associative ring A with unit together with a copy of k in the center of A (whose unit element coincides with that of A). Thus A is a k-vector space and the multiplication map from AxA to A is k-bilinear. Indeed, we could equivalently define a k-algebra as an associative ring A with nonzero unit that has the structure of a k-vector space with bilinear multiplication; the embedding of k into A would then send each field element c to c1=1c where 1 is the unit element of A.
Konkrétne nerozumiem ako sa dostali k vektorovemu priestoru. Thus A is a k-vector space . .
Celemu odstavcu nejak nerozumiem.
Offline
- (téma jako vyřešené označil(a) JohnPeca18)
#3 18. 02. 2013 19:16
- JohnPeca18

- Příspěvky: 651
- Škola: MFF UK
- Pozice: Absolvent 2014
- Reputace: 81
Re: k-algebra
↑ Brano:
Jo je to tam celkom dobre. Aj som to pochopil, len mi vrta hlavou. Keď mám algebru F a v nej nejaké komutatívne pole K. Ako viem, že F sa dá vyjadriť ako vektorový priestor nad K, s bilinearnou formou. Popravde, jediný dôvod, prečo toto rieším je, že sa snažím pochopiť dôkaz Wedderburnovej vety.
http://en.wikipedia.org/wiki/Wedderburn … le_theorem
V dôkaze mám algebru A. V nej nájdem komutatívne podpole Z(A). Tomu rozumiem. No zrazu je tam
Since the center Z(A) of A is a field, A is a vector space over Z(A) with finite dimension n.If q is the order of Z(A), then A has order 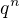 .
.
Offline
#4 18. 02. 2013 19:33 — Editoval Brano (18. 02. 2013 19:48)
Re: k-algebra
No bohuzial s tym ti moc neporadim. Vyzera ze to je nejake zakladne tvrdenie - vo viacerich odkazoch som si vsimol proste pouzite - ako napr.
"Every division ring is therefore a division algebra over its center." tu: http://en.wikipedia.org/wiki/Division_ring
problem je, ze sa to tazko googli ked tomu clovek nepozna meno :-) snad sa ozve nejaky algebraik
Ja by som tu otazku teda formuloval takto:
Nech  je okruh a nech jeho centrum
je okruh a nech jeho centrum 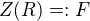 je pole. Za akych podmienok plati, ze
je pole. Za akych podmienok plati, ze  je algebra nad polom
je algebra nad polom  ? (+ nejaky odkaz na literaturu si prosime :-)
? (+ nejaky odkaz na literaturu si prosime :-)
Offline
#5 20. 02. 2013 22:54
Re: k-algebra
JohnPeca18 napsal(a):
ahoj,
Konkrétne nerozumiem ako sa dostali k vektorovemu priestoru. Thus A is a k-vector space . .
Celemu odstavcu nejak nerozumiem.
Na overenie, ze A je vektorovy priestor nad k by sme mali skontrolovat, ci
* 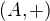 je komutativna grupa
je komutativna grupa
* 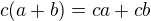 pre
pre 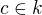 ,
, 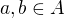
* 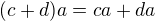 pre
pre 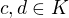 ,
, 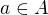
* 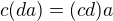 pre
pre 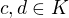 ,
, 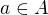
* 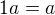
Vsetky tieto vlastnosti platia, lebo  je okruh.
je okruh.
Bilinearita 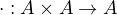 znamena to, ze
znamena to, ze 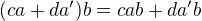 a
a 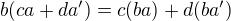 . To tiez ocividne plati. V tej druhej lastnosti sme vyuzili, ze c,d su v centre.
. To tiez ocividne plati. V tej druhej lastnosti sme vyuzili, ze c,d su v centre.
Cize z tej prvej definicie naozaj vyplyva, ze je to vektorovy priestor nad k.
Na ten opacny smer som sa zatial nepozeral. Ale v to dokaze sa zda, ze potrebujes tento.
Ale mozno odpovedam na nieco, co ti uz medzicasom je jasne...
Offline
#6 20. 02. 2013 23:15
Re: k-algebra
↑ JohnPeca18:
Uz tam teda asi chyba iba to preco ma konecnu dimenziu, ale toje jasne z toho, ze ten okruh je konecny.
Offline
#7 21. 02. 2013 08:00
Re: k-algebra
Dôkaz Wederburnovej vety dokonca Aigner a Ziegler vybrali do Proofs from THE BOOK, čo je kniha, kde sa snažili zozbierať veľmi elegantné dôkazy (ale prístupné pre undergraduate študentov). Je to v Chapter 6.
Takže by to mal byť pekný dôkaz, tiež by som si ho mal niekedy pozrieť. (Ak si dobre pamätám, keď nás to učili, tak tam bol nejaký iný dôkaz. Už si ho však nepamätám a neviem, či nájdem niekde poznámky zo svojich školských čias.)
Offline
#8 21. 02. 2013 08:04 — Editoval JohnPeca18 (21. 02. 2013 08:05)
- JohnPeca18

- Příspěvky: 651
- Škola: MFF UK
- Pozice: Absolvent 2014
- Reputace: 81
Re: k-algebra
↑ kompik:
Ďakujem velmi pekne :), nie ešte mi to nebolo známe, učil som sa medzičasom iné dôkazy. Taky
dekuji za reputačný bod, nevím jestli si ho zasloužím, o Weddeburna mám záujem úplne zo zištných dôvodov, potrebujem urobiť skúšku, získať kredity, dokončiť školu .. .
edit: Diky za odkaz pozriem sa na to.
↑ Brano:
Jo, to by už malo stačiť. Díky za pomoc a snahu. Pozerám, že pri odpovedaní zabrousíš teda do široké palety témat.
Offline
 je bilinearna operacia na
je bilinearna operacia na 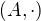 je algebra nad
je algebra nad