Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Aditivní inverze modulo (TOTO TÉMA JE VYŘEŠENÉ)
#1 17. 02. 2013 11:42
Aditivní inverze modulo
Zdravím,
narazil jsem v přednáškách na pojem aditivní inverze modulo (v základech modulární aritmetiky) a bohužel jsem nepochopil, jak ji počítat. Mohl byste mě prosím někdo trknout?
Offline
- (téma jako vyřešené označil(a) mb305)
#2 17. 02. 2013 16:32
Re: Aditivní inverze modulo
Ahoj,
pokud to znamená hledání inverzních prvků v tělese, tak znám 2 způsoby.
1. Pomocí eulerovy věty: platí, že 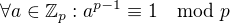 , tudíž pokud dostanu číslo
, tudíž pokud dostanu číslo  , tak jeho inverz je
, tak jeho inverz je 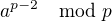 .
.
2. Většinou rychlejší způsob je použít Bézoutovu rovnost: Pokud mám číslo 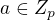 , pak
, pak 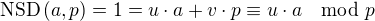 . Čili stačí nalézt číslo
. Čili stačí nalézt číslo  pomocí Euklidova algoritmu.
pomocí Euklidova algoritmu.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Aditivní inverze modulo (TOTO TÉMA JE VYŘEŠENÉ)

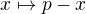
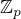 inak by to mohlo byt iba
inak by to mohlo byt iba  (ak by sme uvazovali grupu
(ak by sme uvazovali grupu 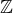 )
)