Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 24. 02. 2013 17:23
#8 24. 02. 2013 17:36 — Editoval Arabela (24. 02. 2013 17:41)
Re: určete definicni obor
↑ Adulka: áno, v menovateli nemůže byř nula; to je podmienka. Ale v našom prípade to ani nikdy nula nie je!
Platí: , z toho
, z toho 
Takže náš výraz v menovateli bude vždy väčší nanajvýš rovný štyrom, a teda nemůže byř nulový.
server.gphmi.sk/~domanyov
Offline
#9 24. 02. 2013 17:36
Re: určete definicni obor
ne.
x^2 nikdy nenybývá záporných hodnot tudíž to nikdy nula nebude.
Řešíš rovnici:


Jinak v R to nemá řešení samozřejmě
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline

 urci D(f) teto f-ce..
urci D(f) teto f-ce..
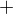

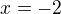 ???
??? nerovná sa
nerovná sa 
 nerovná sa
nerovná sa 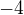
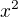 sa predsa nikdy nemůže rovnař zápornému číslu!
sa predsa nikdy nemůže rovnař zápornému číslu!