Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 02. 2013 19:48
Vektory
Vážení, můžete mi prosím pomoci, zas nenalézám nějaký analitický případ...
Zadání: Jsou dány vektory: a=(2,-1,3,5,-4) , b=(0,-4,-6,3,2) , Vypočítejte: a) a+b , b) a-b , c) 2*a , d) a*b , e) |b|
Vůbec nevím, co s tím. Materiály z konzultací velice povrchní.
Děkuji vřele.
Offline
- (téma jako vyřešené označil(a) Alibaba)
#2 24. 02. 2013 19:51 — Editoval ((:-)) (24. 02. 2013 19:52)
#3 25. 02. 2013 09:06
Re: Vektory
Děkuji.
Ovšem já jsem bohužel taky velmi jednoduchý, protože tomu stejně nerozumím.
Kupř. nevím, proč je u "a" i "b" v závorkách 5 čísel a co z toho mám vyvodit. Ostatní příklady mají obvykle do 4. Měl jsem za to, že jde o souřadnice vektorů....Zdá se, že jsem úplně mimo. :(
Offline
#4 25. 02. 2013 10:28
Re: Vektory
↑ Alibaba:
Nejste mimo - jsou to skutečně souřadnice vektorů. Obvykle jsou dvě nebo tři (pokud jsou to vektory v rovině nebo v prostoru), ale může jich být i víc (klidně i deset, sto, dokonce i nekonečně mnoho). V matematice holt není deseti nebo storozměrný prostor ničím neobvyklý. Neděste se z toho, zachází se s tím (až na vektorový součin) úplně stejně jako ve dvou nebo třech rozměrech. Takže je-li a=(2,-1,3,5,-4) , b=(0,-4,-6,3,2), je
a+b = (2+0; -1+(-4); 3+(-6); 5+3; -4+2 )
atd.
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#5 25. 02. 2013 11:48
Re: Vektory
↑ Alibaba:
1. Ak máš zadané vektory a,b a potrebuješ získať súčet týchto vektorov, tak a+b vznikne tak, ze ščítaš odpovedajúce súradníce.
napr.: a(a1,a2,a3)
b(b1,b2,b3)
-----------------------------
a+b=(a1+b1;a2+b2;a3+b3)
a- b=(a1-b1; a2-b2; a3-b3)
_______________________________
2. 2*a získaš prenasobením každej súradnice vektora a číslom 2
a(a1,a2,a3) \Rightarrow 2*a= (2*a1; 2*a2 ; 2*a3)
_______________________________
3. 
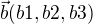
--------------------------------
a*b= (a1*b1 ; a2*b2 ; a3*b3 )
_______________________________
4. \sqrt{b1^{2}+ b2^{2} + b3^{2}}
Pomohol som? Nemusíte ďakovať.
Zvyšenie reputácie postačí. ;-)
Offline
#6 25. 02. 2013 12:05
Re: Vektory
↑ martisek:
Takže jestli jsem to správně pochopil:
a+b = (2+0, -1+(-4), 3+(-6), 5+3, -4+2) = (2, -5, -3, 8, -2)
a-b = a+(-b) = (2-0, -1+4, 3 +6, 5-3, -4-2) = (2, 3, 9, 2, -6)
2a = (2*2, 2*(-1), 2*3, 2*5, 2*(-4)) = (4, -2, 6, 10,-8)
a*b = tady musím postupovat podle vzorce: w = u × v = (u2v3 - u3v2; u3v1 - u1v3; u1v2 - u2v1).
Akorát, že to bude mít 5 kombinací
|b| = tady ještě musím zapracovat...
Offline
