Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#26 01. 03. 2013 10:13 — Editoval Rumburak (01. 03. 2013 10:28)
Re: Kurzweilův integrál
Pokud bychom požadovali jen existenci primitivní funkce, pak by by takto byly integrovatelné i některé funkce nespojité a dokonce i funkce, které nelze integrovat riemannovsky.
To je samozřejmě pravda. Ale mně osobně tato okolnost nijak nezneklidňuje, zase jiné funkce jsou integrovatelné riemannovsky
a nikoliv newtonovsky. Hodně zde záleží na tom, podle jakých zdrojů kdo studoval a jaké představy z nich přejal, jak byl ovlivněn
svými učiteli a pod.
Offline
#27 01. 03. 2013 10:45
Re: Kurzweilův integrál
zaujímavá by mohla (pravdepodobne asi ale nebude) otázka či môže existovať definícia integrálu taká, že každá ohraničená funkcia na ohraničenom intervale by bola podľa tej definície integrovateľná
MATH IS THE BEST!!!
Offline
#28 01. 03. 2013 11:02 — Editoval Rumburak (01. 03. 2013 11:08)
Re: Kurzweilův integrál
↑ jarrro:
Ahoj. Pokud by taková definice existovala, pak by pro každou omezenou množinu byla definována její míra jakožto integrál
z charakteristické funkce této množiny. Takováto míra by ale nemohla mít všechny z vlastností Lebesgueovy míry, protože
existují množiny Lebesgeovsky neměřitelné (ač omezené). Museli bychm tady poněkud změnit své intuitivní představy
o míře množin, z nichž teorie Lebesgueovy míry vychází.
Offline
#29 01. 03. 2013 11:22
Re: Kurzweilův integrál
↑ Rumburak:tá definícia by nemusela byť Lebesguovho typu.
či to myslíš tak, že ak by ten nový integrál spĺňal sigma aditivitu pre každú funkciu teda, že pre každé spočítateľné delenie intervalu by platilo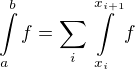
tak by množinová funkcia definovaná rovnosťou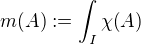
mala vlastnosti miery a pokiaľ by nový integrál mal v prípade aj Lebesguovsky integrovateľných funkcií hodnotu integrálu zachovať tak by m bola rozšírenie Lebesguovej miery na všetky ohraničené množiny čo by dalo spor s axiómou výberu?
chápem to správne?
MATH IS THE BEST!!!
Offline
#30 01. 03. 2013 11:52 — Editoval Rumburak (01. 03. 2013 16:22)
Re: Kurzweilův integrál
↑ jarrro:
Myslel jsem to v podstatě tak, jak popisuješ.
Možná víš, že abstraktní Lebesgueův integrál se dá vybudovat nejen "zdola" vycházejíce z teorie míry, ale též axiomaticky, kdy
integrál je vzat jako primitivní pojem, jemuž jsou přisouzeny určité axiomy popisující nejobecnější vlasnosti integrálu. Této teori
se říká Danielův integrál (možná Daniellův). Při vhodně volbě axiomů dostaneme teorii, které je ekvivelentní teorii Lebesgeově
budované "zdola".
Nemám to ale natolik prostudováno, abych mohl říci, které "přirozené" vlastnosti integrálů bychom se při jeho definici museli vzdát,
abychom se výše popsanému sporu s axiomem výběru vyhnuli.
Offline
#31 01. 03. 2013 12:20
Re: Kurzweilův integrál
↑ Rumburak:
Samozřejmě - pokud se vyjasní definice, tak o nic nejde. Zajímavé je, že něco podobného řešíme občas i s derivací. Když třeba na derivaci přijde řeč u státnic a adept u definiční limity zapomene slůvko "vlastní" (to není nic proti ničemu - občas se připouštějí i nevlastní derivace), tak se zeptám na derivaci funkce signum v nule. Ona pak kupodivu existuje - je plus nekonečno. To většinou překvapí i ty, kteří nevlastní derivace připouštějí jako derivace definující svislé tečny resp. polotečny.
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#32 01. 03. 2013 14:19
Re: Kurzweilův integrál
↑ martisek:
Ona takto derivacia vie mat aj hlbsi zmysel. V ramci teorie distribucii je to 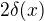 ak sa nemylim, kde
ak sa nemylim, kde 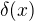 je Diracova delta funkcia.
je Diracova delta funkcia.
Offline
#33 02. 03. 2013 10:46 Příspěvek uživatele Rumburak byl skryt uživatelem Rumburak. Důvod: Byl to nesmysl.
#34 02. 03. 2013 11:38 — Editoval Pavel Brožek (02. 03. 2013 11:39)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Kurzweilův integrál
↑ Rumburak:
Proč by nás měl vůbec součin 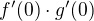 zajímat? V souvislosti s větou o derivaci součinu funkcí by nás spíš měl zajímat výraz
zajímat? V souvislosti s větou o derivaci součinu funkcí by nás spíš měl zajímat výraz 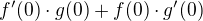 , který smysl nemá.
, který smysl nemá.
Poznámka k distribucím: Jestli se nepletu, tak jakmile se začneme bavit o derivování ve smyslu distribucí, tak pak nemá smysl se vůbec ptát na derivaci v nějakém bodě, protože distribuce nejdou funkce, které by každému bodu přiřazovaly jiný bod. Nemá teda asi moc smysl psát např.  , jen
, jen 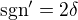 .
.
Offline
#35 02. 03. 2013 11:43
Re: Kurzweilův integrál
↑ Pavel Brožek:
No já jsem už asi dementní. Spletl jsem si to s větou o LIMITĚ součinu. Díky za upozornění.
Offline