Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 03. 2013 10:25 — Editoval Carnage (02. 03. 2013 10:26)
Kombinace:rovnice, nerovnice
Cau, potřeboval bych poradit se dvěma příklady, sám už si nevím rady tak se obracím na Vás
a)
(n nad 2)+(n+3 nad 2) +(n+6 nad 2) ≤ 72
b)

(omlouvám se všem za zápis)
Offline
- (téma jako vyřešené označil(a) Carnage)
#2 02. 03. 2013 10:42 — Editoval Aquabellla (02. 03. 2013 10:46)
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Kombinace:rovnice, nerovnice
↑ Carnage:
a) 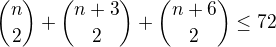
Doporučuji si přepsat jednotlivá kombinační čísla jako zlomek s faktoriály: 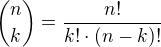
Například pro první kombinační číslo to vypadá takto: 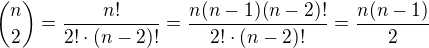
b) 
To samé jako v předchozím příkladě.
Kombinační čísla bez proměnné x jde rovnou vyčíslit jako přirozená čísla.
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
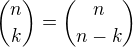 , kde n = x+1
, kde n = x+1