Matematické Fórum

Hopsalin · 03. 03. 2013 13:50

log čísla z se základem 10 - 2 = 6 * log na -1 čísla z - 1 se základem 10

Prosím o vyřešení tohoto příkladu nevím jak se zbavit toho na log -1.

Děkuji moc.

marnes · 03. 03. 2013 13:53

↑ Hopsalin:
$\log_{}z-2=6\log_{}^{-1}(z-1)$ takto?

((:-)) · 03. 03. 2013 13:53 — Editoval ((:-)) (03. 03. 2013 13:54)

↑ Hopsalin:

Mal by si si naštudovať pravidlá práce s logaritmami ...

Freedy · 03. 03. 2013 13:53

$\log_{}z - 2 = 6*\log_{}^{-1}(z-1)$

takto?

Arabela

Ahoj ↑ Hopsalin:,
máme teda rovnicu
$\log_{}z-2=6\log_{}^{-1}z$ ,
čo znamená vlastne
$\log_{}z-2=6(\log_{}z)^{-1}$ , resp.
$\log_{}z-2=6.\frac{1}{\log_{}z}$ .
Prenásobíš menovateľom, po substitúcii
$u=\log_{}z$
dostaneš kvadratickú rovnicu, ...
EDIT: To -1 na pravej strane som si nevšimla... Alebo tam predtým nebolo?...

Martin95k

Ahoj, šlo by to teda upravit: $\log_{}z-\frac{6}{\log_{}[z-1]}=2$
Toto je otázka, ne odpověď... :D Díky

marnes · 03. 03. 2013 14:15

↑ Martin95k:
ano. Ale autor ještě nereagoval, zda je to zadání správné

Hopsalin · 03. 03. 2013 14:20

takhle je to zapsáno dobře akorát to z-1 nemá být v závorce.

Hopsalin · 03. 03. 2013 14:21

U freedyho

marnes · 03. 03. 2013 14:22 — Editoval marnes (03. 03. 2013 14:23)

$\log_{}z - 2 = 6*\log_{}^{-1}z-1$

takže takto?

pokud ano, tak zaveď substituci za logz=y, vyřeš a vrať se do substituce

Hopsalin · 03. 03. 2013 14:27

Ano takhle. Jen jestli bych mohl poprosit o podrobnější popis jelikož s tohodle nejsem moc chytrý.

Děkuji.

((:-)) · 03. 03. 2013 14:32

↑ Hopsalin:

Tie pravidlá práce s logaritmami si si pozrel? Odkazujem na ne v príspevku číslo 3.

Martin95k

Já postupoval takto: $\log z-\frac{6}{\log_{}z}=1$
substituce: $y=\log_{}z$ $y-\frac{6}{y}-1=0$
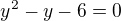rce po vynásobením y: $y^{2}-y-6=0$ nulové body: $y_{1}=-2$ a $y_{2}=3$
dosazení do substituce: $\log_{}z=3$ .... $z=1000$
$\log_{}z=-2$ ..... $z=\frac{1}{100}$
Snad je to dobře.