Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 03. 03. 2013 11:57
Re: Vyšetření průběhu funkce
Určit defeniční obor funkce, určit vlastnosti (sudost, lichost, periodicita...), vyšetřit spojitost, určit průsečíky s osami, určit limity v nevlastních a nedefinovaných bodech, udělat první derivace, zjistit kde funkce roste, kde klesá, kde má maximum/minimum, popřípadě druhou derivaci a najít inflexní body + konkávnost konvexnost, asymptoty...
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#5 03. 03. 2013 15:31
Re: Vyšetření průběhu funkce
↑ Martin95k: funkce je spojitá když platí
Takže například funkce:
je spojitá na celém Df. Protože platí pro každé a
Ale například funkce: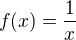
není spojitá v nule, protože nulou se nedá dělit.
Tudíž neplatí že:
Dá se to vyčíst z grafu, nebo podle funkčního předpisu apodobně.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#6 03. 03. 2013 16:01
Re: Vyšetření průběhu funkce
↑ Freedy: Šlo by tedy jendnoduše říct, že pokud fce má nějaké jednostranné limity, ve kterých není definována, pak není spojitá?
Např: 
..vydíme, že 
...můžeme tvrdit, že fce není spojitá
ale 
...
...fce je spojitá
Lze to takhle jednoduše tvrdit bez použití limit?
Díky za odpověď
Offline
#7 03. 03. 2013 16:11 — Editoval Freedy (03. 03. 2013 16:33)
Re: Vyšetření průběhu funkce
ano, lze to tvrdit i tak, že pokud je funkce v nějakém bodě nedefinovaná, ale je definována v okolí tohoto bodo (zprava i zleva) tak je funkce nespojitá
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline