Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 04. 03. 2013 20:43 — Editoval vanok (05. 03. 2013 02:01)
Re: kvadratické rovnice v c
Ahoj ↑ lotoska:,
Mas tam malu nepozornost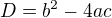
À tiez
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 04. 03. 2013 20:53 — Editoval lotoska (04. 03. 2013 21:23)
Re: kvadratické rovnice v c
↑ lotoska:
tak v tom případě, mám i tu předchozí rovnici před touto rovnicí vypočtenou špatně ?
V předchozím, již uzavřeném příkladě?
tento příklad tedy 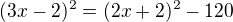
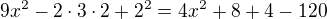
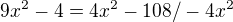
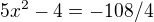
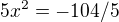
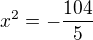
x1=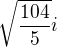
x2=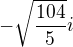
TAKHLE BY TO TEDY MĚLO BÝT?
Offline
#5 04. 03. 2013 21:41
#6 04. 03. 2013 21:55 — Editoval Pivňa (04. 03. 2013 22:06)
Re: kvadratické rovnice v c
špatně používáš následující vzorec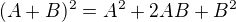
pro dvojčlen na levé straně
A= 3x
B= -2
tedy 
to samé použij na dvojčlen napravo, posčítej odpovídající si členy a sestav kvadratickou rovnici
(edit: pokud mám B= -2, pak je zápis +- zmatečný => odstranění +- )
Offline
#8 04. 03. 2013 22:03
#9 04. 03. 2013 22:08
Re: kvadratické rovnice v c
Offline

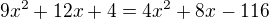 /
/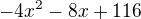
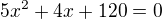
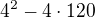
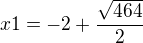

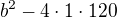
 -20X+120=0
-20X+120=0