Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 06. 03. 2013 19:19
Re: složené derivace
↑ bonifax:
ajo je to pí nemohla sem to přečíst jak nam to ucitelka skenuje na stranky takže jak když je tam to pí
Offline

 udělám substituci
udělám substituci  zderivuji
zderivuji  mám to dobře dotěd?? a co dál s tím musím nějak rozložit ten první jmenovatel??
mám to dobře dotěd?? a co dál s tím musím nějak rozložit ten první jmenovatel??



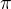 v zadání ?:)
v zadání ?:) - vnější funkce,
- vnější funkce,  - vnitřní funkce
- vnitřní funkce





 je 0? je to jakonormální číslo?
je 0? je to jakonormální číslo?