Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 25. 12. 2008 13:49
Kruhová trajektorie
Zdravím,
řeším jeden příklad, výsledek mám správně, ale nejsem si jistý, jestli jsem něco neopomenul.
př.: Jak velkou rychlost je třeba uděliit nějakému tělesu ve výšce h = 500km nad zemským povrchem, aby se pohybovalo jako umělá družice Země po kruhové trajektrorii?
do vzorečku  jsem dosadil hodnoty a vyšlo mi
jsem dosadil hodnoty a vyšlo mi
7,2 * 10^3 km/s. Což je podle skript správně.
Ale učitel mi do příkladu připsal ještě poznámku: Rozmyslete si pečlivě, jak k řešení přistoupit - se správným způsobem je vskutku jednoduchý. Nezapomeňte, že v takto velkých výškách již musíme pro gravitační sílu použít Newtonův gravitační zákon.
ten zní:  , kde G= 6,67·10-11 m^3·kg^-1·s^-2. Jenže neznám hmotnost prvního hmotného bodu, jen Země.
, kde G= 6,67·10-11 m^3·kg^-1·s^-2. Jenže neznám hmotnost prvního hmotného bodu, jen Země.
Poraďte prosím.
Oh my god, it's wescoast!
Cokoliv na prvou je cokoliv.
Offline
#2 25. 12. 2008 13:58
Re: Kruhová trajektorie
↑ wescoast:Většinou se hmotnost tělesa vůči hmotnosti Země zanedbává, tudíž se s hmotností tělesa nepočítá , vzorec se pak zjednoduší na  , kde
, kde 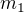 je hmotnost tělesa.
je hmotnost tělesa.
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#5 25. 12. 2008 14:29
Re: Kruhová trajektorie
↑ Ivana:
Já se obávám, že to trochu motáš. Když z toho vzorce vyškrtneme hmotnost tělesa, tak už se nejedná o vzorec pro gravitační sílu, ale o intenzitu gravitačního pole (tj. zrychlení). To, co ve skutečnosti zanedbáváme, je gravitační přitahování Země k tělesu. Pokud počítáme se silami, brzy dojdeme k tomu, že na hmotnosti tělesa nezáleží.
Jde o to, že síla dostředivá je rovna síle gravitační, tj.
Offline
#7 25. 12. 2008 15:52
Re: Kruhová trajektorie
Zdravím,
súhlasím z tým riešením, len by som ešte doplnil, že vo vzorci  je r polomer zakrivenia trajektórie telesa. U kružnice je to síce to isté, čo r vo vzorci
je r polomer zakrivenia trajektórie telesa. U kružnice je to síce to isté, čo r vo vzorci  , ale len tak pre budúcnosť ak by si počítal povedzme príklad s elipsou, tak to už celkom tak nevíde.
, ale len tak pre budúcnosť ak by si počítal povedzme príklad s elipsou, tak to už celkom tak nevíde.
You know who
(or maybe not)
Offline
#9 26. 12. 2008 11:34
Offline
#10 26. 12. 2008 12:09 — Editoval wescoast (26. 12. 2008 12:30)
Re: Kruhová trajektorie
↑ Ivana:
Bohužel je tam chyba, ale úvaha je správná. Poloměr Zěme je 6378, to ano. Jenže k tomu musíš ještě přičíst tu výšku - 500km. Protože jsi jí nepřičetla, tak je jasné, že ti vyšla 1. kosmická rychlost, protože ta funguje tak, když to těleso je ve výšce zanedbatelné, čili jako by leželo na Zemi.
Oh my god, it's wescoast!
Cokoliv na prvou je cokoliv.
Offline
#11 26. 12. 2008 14:07
Re: Kruhová trajektorie
Ivana napsal(a):
↑ wescoast:Ale já jsem tam tu výšku přičetla :
a stoto výškou jsem počítala.
Země má průměr: 12756,3 km,
z toho je poloměr: 6378km
k tomu 5OOkm: 6878km.
Oh my god, it's wescoast!
Cokoliv na prvou je cokoliv.
Offline
#12 26. 12. 2008 20:35
Re: Kruhová trajektorie
↑ wescoast:No máš pravdu, spletla jsem délkové jednotky.:-(
Přepočítala jsem to , ale stejně mi nevyjde  ...ale
...ale  . Je možné, že by výsledek ve skriptech byl špatně- nvynechána ..6 na místě desetin.
. Je možné, že by výsledek ve skriptech byl špatně- nvynechána ..6 na místě desetin.
tady je výpočet i s postupem :
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#14 26. 12. 2008 20:59
Re: Kruhová trajektorie
↑ wescoast:Ano, mně výsledek vyšel přesně :
7,6279093 km/s .. což se dá zaokrouhlit na 7,628 km/s :-)
Jedna krát jedna je " tisíckrát " jedna :-)
Offline

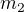 je hmotnost Země .
je hmotnost Země .