Matematické Fórum

Honza90 · 13. 03. 2013 19:49

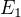Dobrý večer. Mým cílem je ukázat, že, je-li $E$ lineární prostor a $E_{1}$ jeho podprostor, 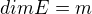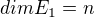$dimE=m$ , $dimE_{1}=n$ , pak dimenze faktorprostoru 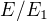$E/E_{1}$ je rovna $m-n$ .

Faktor prostor mám definován jako lineární prostor, jehož prvky jsou třídy ekvivalence z relace 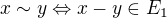$x\sim y \Leftrightarrow x-y\in E_{1}$ pro $\forall x,y\in E$ .
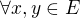Přímo z definice plyne, že třída je vlastně toto $[x_{i}]=E_{1}+y_{i}$ , tedy těch "bázových tříd" faktorprostoru musí být přesně tolik, o kolik dimenzí ten $y$ rozšíří $E_{1}$ .

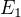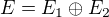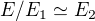Napadlo mě použít ke korektnějšímu důkazu větu o direktním součtu podprostorů: Pokud $E=E_{1}\oplus E_{2}$ , pak $E/E_{1}\simeq E_{2}$ , tedy přirozeně platí, že 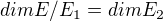$dimE/E_{1}= dimE_{2}$ . Takže bych zkrátka řekl, že můj prostor E je direktním součtem podprostorů E1 a E\E1(E mínus E1), tedy dimenze E mínus E1 je rovna m-n, podle zmíněné věty také dimenze faktorprostoru E/E1 je rovna m-n.
Co vy na to? :)

Brano · 13. 03. 2013 20:01 — Editoval Brano (13. 03. 2013 20:03)

Ty by si potreboval opacne tvrdenie t.j.
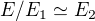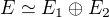Ak $E/E_{1}\simeq E_{2}$ potom $E\simeq E_{1}\oplus E_{2}$ , resp. kratsie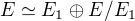 $E\simeq E_{1}\oplus E/E_{1}$
co je vlastne to co tvrdis tu

Honza90 napsal(a):
...
tedy těch "bázových tříd" faktorprostoru musí být přesně tolik, o kolik dimenzí ten $y$ rozšíří $E_{1}$ .
...

len to treba formalne dokazat, ale to nie je tazke.

Honza90

↑ Brano:
nějak formálně to zformulovat se mi právě vůbec nedaří

příjde mi takový divný napsat tohleto $E_{1}+y_{i}$

Brano · 14. 03. 2013 00:36 — Editoval Brano (14. 03. 2013 00:40)

Takze takto:
Najdes bazu 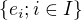$E_1$ .. $\{e_i;i\in I\}$ a treba si uvedomit, ze sa da najst baza 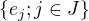$E$ .. $\{e_j;j\in J\}$ taka, ze obsahuje bazu $E_1$ t.j. $I\subset J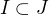$ - to je nejaka zakladna veta o bazach, predpokladam, ze ste ju mali, vychadza z Zornovej lemy. A teraz si uz staci uvedomit, ze 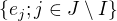$\{e_j;j\in J\setminus I\}$ generuje 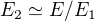$E_2\simeq E/E_1$ a mas hned aj dosledok o pocte prvkov bazy.

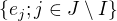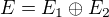Resp. mozno bude lahsie vidiet, ze $\{e_j;j\in J\setminus I\}$ generuje $E_2$ take, ze $E=E_1\oplus E_2$ a potom pouzijes to svoje tvrdenie ze 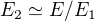$E_2\simeq E/E_1$ a pocet prvkov bazy je hned vidiet.

Matematické Fórum

#1 13. 03. 2013 19:49

faktorprostor

#2 13. 03. 2013 20:01 — Editoval Brano (13. 03. 2013 20:03)

Re: faktorprostor

Honza90 napsal(a):

#3 13. 03. 2013 20:08 — Editoval Honza90 (13. 03. 2013 20:10)

Re: faktorprostor

#4 14. 03. 2013 00:36 — Editoval Brano (14. 03. 2013 00:40)

Re: faktorprostor

Zápatí