Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 14. 03. 2013 16:43
Re: izomorfizmus těles
Ahoj ↑ Honza90:,
Staci poznamenat, ze 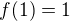
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 14. 03. 2013 18:00
Re: izomorfizmus těles
Ako by si dokazal, ze plati f(2)=2?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 14. 03. 2013 20:38 — Editoval vanok (14. 03. 2013 20:39)
Re: izomorfizmus těles
v tvojom texte, ked pises  , normalne je tym myslene,
, normalne je tym myslene,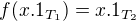 .
.
V pripade, ze by si postupoval kror po kroku, podla indikacii co by som ti dal postupne, by si prisiel sam na to ze tvoj vyrok plati.
Od kial mas ten problem?
Poznamka: priklad je uz vyriesene cvicenie, ktorym sa ilustruje nejaka veta alebo definicia... tak preto pouzivam slovo cvicenie, uloha...
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 14. 03. 2013 21:07
Re: izomorfizmus těles
↑ vanok:
je to ze skript "obecná algebra", ani můj cvičící si s tím nevěděl rady. je určitě podtělesem
je určitě podtělesem  , mají tedy stejnou jedničku, je to číslo
, mají tedy stejnou jedničku, je to číslo  , stejně tak všechny podtělesa
, stejně tak všechny podtělesa  budou mít tuto jedničku, proto jak píšeš vždy platí
budou mít tuto jedničku, proto jak píšeš vždy platí 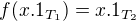 . čili
. čili  . Tak?
. Tak?
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#8 14. 03. 2013 23:24
Re: izomorfizmus těles
Ano.
A preto mas aj f(1+1)=f(1)+f(1)=1+1=2
Teraz by bolo dobre si primomenut ako sa konstruhuje Q. Napis.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 15. 03. 2013 13:09
Re: izomorfizmus těles
↑ Honza90:, prave to treba vyuzit, presne ako to uz naznacil kolega ↑ Brano:.
Ja som ti dal cestu, ako sa dostat k Z.... v obraze.
A Brano ti naznacil cestu ku Q.
Tak daj to vsetko dokopy...
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

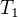 a
a 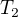 jsou podtělesa tělesa
jsou podtělesa tělesa  je izomorfismus tělesa
je izomorfismus tělesa  .
.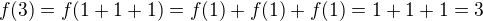
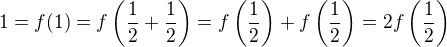 atd :-)
atd :-)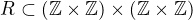 kde
kde 