Matematické Fórum

wolfito · 17. 03. 2013 15:56

Zdravíčko,
Hodíme dvakrat kostkou. Jaka je pravdepodobnost že,
a) padne alespon jednou liche cislo?
$\frac{3}{6}*\frac{3}{6}=\frac{1}{4}=25\%$
b)soucet vetsi nez deset.
$\frac{2}{6}*\frac{2}{6}=\frac{1}{9}=11\%$
Je to dobře?

brodzko · 17. 03. 2013 16:04

Ahoj,

povedal by som, že nie. V a) sa pýtajú na pravdepodobnosť, že nepárne číslo padne aspoň raz - ja by som uvažoval o troch prípadoch:

1) padne N + P
2) padne P + N
3) padne N + N

a sčítal všetky tieto pravdepodobnosti. Teda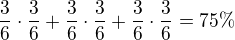

$\frac{3}{6}\cdot \frac{3}{6} + \frac{3}{6}\cdot \frac{3}{6} + \frac{3}{6}\cdot \frac{3}{6} = 75\%$

Pokiaľ ide o b) treba nájsť všetky možnosti ktorých súčet je väčší než 10 (6 + 6, 6 + 5, 5 + 6) a klasicky zrátať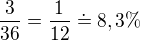

$\frac{3}{36} = \frac{1}{12} \doteq 8,3\%$

Môže byť? :)

wolfito · 17. 03. 2013 16:09

↑ brodzko:
No nejsem si jist tím za a)

brodzko · 17. 03. 2013 16:19

Nech sa teda vyjadrí aj niekto ďalší. Ja si myslím že ty si vyrátal presný opak - pravdepodobnosť že nepadne žiadne nepárne číslo - už keď si uvedomíš že stačí ak padne nepárne číslo na ktorejkoľvek z dvoch kociek alebo na oboch, pravdepodobnosť musí byť vyššia :)

wolfito · 17. 03. 2013 16:26

ALe asi mas pravdu, dik ;)

Matematické Fórum

#1 17. 03. 2013 15:56

Pravdepodobnost

#2 17. 03. 2013 16:04

Re: Pravdepodobnost

#3 17. 03. 2013 16:09

Re: Pravdepodobnost

#4 17. 03. 2013 16:19

Re: Pravdepodobnost

#5 17. 03. 2013 16:26

Re: Pravdepodobnost

Zápatí