Matematické Fórum

salmi · 17. 03. 2013 18:05

ahoj,

potřebovala bych poradit s následujícím příkladem, seděla jsem nad ním půl hodiny, ale nic moc jsem nevykoumala, zadání je následující:

Sestrojte trojúhelník ABC, pokud znáte $r, v_{a}, \varkappa$ a platí, že $\varkappa = (0,\Pi )$ . Proveďte diskuzi.

Asi bude záležet, zda bude střed stejnolehlosti totožný se středem kružnice trojúhelníku opsané či nikoliv. Zkoušela jsem sestrojit kružnici, její obraz ve stejnolehlosti, dále zvolit libovolně bod A, určit jeho obraz, ale dál jsem si nevěděla rady... Někdo nějaký nápad? Předem moc díky.

martisek

↑ salmi:

Co je $\varkappa$ ? Předpokládám, že nejaký úhel. Jaký?

salmi · 17. 03. 2013 19:00

ne, to je značka pro stejnolehlost, asi jsem měla spíše použít tento znak $\chi$

martisek · 17. 03. 2013 19:02

↑ salmi:

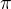No, jo, ale pak nechápu $\varkappa = (0,\Pi )$ . To jako střed je v počátku a koeficient je $\pi$ ? A co má ta stejnolehlost společného s tím trojúhelníkem?

salmi · 17. 03. 2013 19:07

ano, střed je v 0 a koeficient je $\pi$ ... takhle znělo zadání... pravděpodobně má ta stejnolehlost posloužit ke konstrukci, jelikož jen na základě poloměru a výšky trojúhelník asi nezkonstruuji...

martisek

↑ salmi:

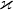Tak buď něco nechápu, anebo je to nějaký nesmysl. Trojúhelníků o známé $r, v_{a}$ je obecně nekonečně mnoho a co s tím má společného ta stejnolehlost, to mi ze zadání není jasné. Trojúhelník nelze zadat dvěma prvky a stejnolehlostí, která s ním nemá nic společného. Nemá to $\varkappa$ být nějaký úhel o velikosti z intervalu $(0,\pi )$ ?

salmi · 17. 03. 2013 19:44

no, je to možné, ono tam nic k tomu napsáno nebylo (jakože je to stejnolehlost nebo úhel), vyfotím sem to zadání... ale nevím, od kdy se úhel v trojúhelníku zadává pod tímto řeckým písmenem, okamžitě mě totiž napadla značka stejnolehlosti, která je totožná...

DUMAG · 17. 03. 2013 19:57

salmi:
Keďže neviem čo je presne stejnolehlost skús to skonštruovať nasledovne:
A.) ak trojuholník je rovnoramený:

1. narysuj výšku va,označ body úsečky napr. C,D
2.narysuj kružnicu s polomerom r,tak aby prechádzala bodom D.
3.bodom D veď dotyčnicu ku kružnici
4.z bodu C veď dotyčnice ku kružnici,kde pretnú dotyčnicu,ktorá prechádza bodom D sú body B a D

B.)ak trojuholník je rovnostrany:

1.narysuj va v 1/3 je stred S kružnice opísanej trojuholníku
2.narysuj kružnicu s polomerom r= 2/3 va - musí prechádzať bodom výšky- bod trojuholníka napr.C
3.narysuj kolmicu druhým bodom výšky na výšku.Priesečníky kružnice a kolmice sú body trojuholníka A a B.
vznikol rovnostraný trojuholník
Prípadne mi definuj stejnolehlost

salmi · 17. 03. 2013 23:25

toto je zadani, je to Pr. 1... ale jak tak koukam na ty ostatni priklady, asi to opravdu bude znamenat jen uhel, otazkou je, jaky?

martisek

↑ salmi:

No, vidím, že zrovna ten první příklad je zadaný dost lajdácky a zadání se (bohužel) bude muset trochu domyslet. Především to 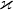$\varkappa$ není $\varkappa =$ , ale $\varkappa \in$ . To znamená, že je to nějaká hodnota, ležící v intervalu $(0,\pi )$ , takže se dá odhadnout, že to bude úhel. Jaký úhel - to už je opravdu spekulace, ale dovolil bych si odhadnout, že $\gamma$ (tomu se to tak nejvíc podobá).

Je-li tomu tak, pak je situace následující. Má se sestrojit černý trojúhelník ABC, jsou-li zadány červené prvky:

Takže bych začal libovolně umístěným úhlem $\gamma$ s vrcholem C, s jehož ramenem a sestrojíme rovnoběžku a' ve vzdálenosti v_a. Vrchol A získáme jako průsečík přímek b, a'. Dále sestrojíme bod S jako vrchol rovnoramenného trojúhelníka se základnou AC, pro jehož ramena je AS=CS=r. Konečně sestrojíme kružnici se středem v bodě S a poloměrem r - ta bude procházet již známými body A, C a přímku a protne navíc v hledaném bodě B.

Všechny kroky konstrukce jsou proveditelné jednoznačně až na jediný: Vyjde-li strana AC delší než průměr kružnice, nebude možné sestrojit bod S. Protože $|AC| = \frac {v_a} {\sin\gamma}$ , nebude mít úloha řešení pro $2r< \frac {v_a} {\sin\gamma}$ . Úloha dále nebude řešitelná pro $\gamma \ge \frac {\pi} 2$ - v tom případě totiž bod B (i když ho sestrojíme) buď splyne s C, anebo bude ležet na opačné polopřímce k ramenu úhlu $\gamma$ a takto sestrojený trojúhelník by neměl úhel $\gamma$ , ale $\pi - \gamma$

Ve všech ostatních případech má úloha právě jedno řešení.

V každém případě by to ale chtělo zjistit, co je opravdu myšleno tím 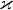$\varkappa$ . S tím úhlem $\gamma$ samozřejmě nemusím mít pravdu...