Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 03. 2013 18:11
- Kouří se mi v hlavě
- Příspěvky: 82
- Reputace: 1
M a T i C e
Ahoj,
mám menší problém s úkolem, zadání je zde: 
Vím, že...
1) 
2) 
tzn. získávám:  , není to blbost?
, není to blbost?
i.) Pak  bude platit, protože matice = 1 na jakékoliv přirozené číslo dá vždycky 1, je to tak?
bude platit, protože matice = 1 na jakékoliv přirozené číslo dá vždycky 1, je to tak?
ii.) No a to pak samozřejmě taky platí...
Sakra, teď mi došlo, že takové úpravy s maticemi nemůžu provádět.
Skončil jsem tady: 
Nevím, jak dál :((
Poradil by prosím někdo?
Díky moc.
Offline
- (téma jako vyřešené označil(a) Kouří se mi v hlavě)
#2 16. 03. 2013 23:52 — Editoval Brano (16. 03. 2013 23:54)
Re: M a T i C e
Ak by existovalo 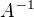 tak by si mal
tak by si mal  co sice je trivialna projekcia, ale tento priklad je zrejme vseobecnejsi.
co sice je trivialna projekcia, ale tento priklad je zrejme vseobecnejsi.  nemusi byt ani stvorcova, teda ani
nemusi byt ani stvorcova, teda ani 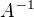 ani
ani  nema (nemusi) mat zmysel.
nema (nemusi) mat zmysel.
definicia:  je matica ortogonalnej projekcie prave vtedy ked
je matica ortogonalnej projekcie prave vtedy ked  a
a 
toto si mozes lahko overit
to druhe je podobne trivialne.
No a potom sa lahko ukaze  idukciou - indukcny krok je
idukciou - indukcny krok je 
Offline
#3 18. 03. 2013 20:16
- Kouří se mi v hlavě
- Příspěvky: 82
- Reputace: 1
Re: M a T i C e
↑ Brano:
Velké díky! Moc mi to pomohlo!
Ta transpozice mi dělá trochu problémy, ukážu co mám...
Jsem si jistý tímhle: 
Teď doplnit závorku...
Pamatuju si odněkud tvrzení, že 
...a 
Offline
#5 18. 03. 2013 21:46 — Editoval Kouří se mi v hlavě (18. 03. 2013 21:49)
- Kouří se mi v hlavě
- Příspěvky: 82
- Reputace: 1
Re: M a T i C e
↑ Brano:
Jé, díky!
A pokud matice splňuje výše uvedené...
pak to znamená, že jde o projekci, tj. zobrazení x-rozměrného prostoru do y-rozmerného prostoru, kde y < x?
A jestliže existuje n-rozměrný prostor, existují i vektory, pak i matice, které vektory převádějí... a jestliže zároveň ty matice splňují i. a ii. bod, tak je to projekce?
To je asi dost pitomá ukázka té druhé části...
Co myslíš?
P.S.
Neumím moc dokazovat... ty ses to tak hezky naučil cvikem a časem? (nebo jsi přirozený talent?)
Offline
#6 19. 03. 2013 01:07
Re: M a T i C e
Ak matica  (typu
(typu 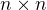 ) splna
) splna  tak je to matica projekcie na nejaky podpriestor
tak je to matica projekcie na nejaky podpriestor  - ono je to v podstate definicia projekcie. Ak naviac
- ono je to v podstate definicia projekcie. Ak naviac  tak sa jedna o ortogonalnu projekciu. Az tvojho zadania tipujem, ze ked sa tam povie projekcia tak sa automatcky mysli ortogonalna projekcia (aj ked takato konvencia nie je vseobecne prijimana, tak je v poriadku.)
tak sa jedna o ortogonalnu projekciu. Az tvojho zadania tipujem, ze ked sa tam povie projekcia tak sa automatcky mysli ortogonalna projekcia (aj ked takato konvencia nie je vseobecne prijimana, tak je v poriadku.)
Ono v vseobecnosti ak  je nejaky priestor, tak
je nejaky priestor, tak  je projekcia, ak
je projekcia, ak  je podpriestor
je podpriestor  a
a  zachovava strukturu (v tomto pripade, ze je to linearne zobrazenie) a pre vsetky
zachovava strukturu (v tomto pripade, ze je to linearne zobrazenie) a pre vsetky  plati
plati  , alebo ekvivalentne pre vsetky
, alebo ekvivalentne pre vsetky  plati
plati  .
.
Nozes si precitat nieco aj tu.
P.S. ano chce to cvik a asi aj pozerat si ako su veci dokazovane v ucebniciach a ako je tam tak celkovo budovana teoria.
Offline
#7 19. 03. 2013 18:49
- Kouří se mi v hlavě
- Příspěvky: 82
- Reputace: 1
Re: M a T i C e
↑ Brano:
Díky za tu anglickou Wiki, to mě vůbec nenapadlo!
Moc dík za všechno, hned je mi to jasnější!
Offline

 je regularna t.j. existuje
je regularna t.j. existuje  potom
potom  je regularna a plati
je regularna a plati  . Ty to potom znacis
. Ty to potom znacis  ale to asi nie je uplne rozsirene znacenie (aj ked je v poriadku). No a potom samozrejme
ale to asi nie je uplne rozsirene znacenie (aj ked je v poriadku). No a potom samozrejme  a
a  .
. .
. tak
tak  .
.