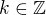Matematické Fórum

bejf · 19. 03. 2013 18:22 — Editoval bejf (19. 03. 2013 18:25)

Ahoj, potřeboval bych opět poradit s jedním příkladem. Uvedl bych postup.
Zadání:
Řešte v $\mathbb{R}$ rovnici:
$sinx+\sqrt{3}cosx=\sqrt{2}$
Můj postup:
$\sqrt{3}cosx=\sqrt{2}-sinx$
Umocním na druhou - pak na konci budu muset provést zkoušku. Teď zatím dostanu:
$3cos^2x=2-2\sqrt{2}sinx+sin^2x\nl 3(1-sin^2x)-sin^2x+2\sqrt{2}sinx-2=0\nl 3-3sin^2x-sin^2x+2\sqrt{2}sinx-2=0\nl -4sin^2x+2\sqrt{2}sinx+1=0\nl 4sin^2x-2\sqrt{2}sinx-1=0$
Použiju substituci $sinx=y$ a dostanu kvadratickou rovnici:
$4y^2-2\sqrt{2}y-1=0\nl D=(-2\sqrt{2})^2-4*4*(-1)=8+16=24\nl y_{1,2}=\frac{2\sqrt{2}\pm\sqrt{24}}{8}=\frac{2\sqrt{2}\pm2\sqrt{6}}{8}=\frac{2(\sqrt{2}\pm\sqrt{6})}{8}=\frac{\sqrt{2}\pm\sqrt{6}}{4}$

A tady jsem zatím skončil, už nevím jak dál. Postup jsem si zkoušel několikrát kontrolovat, snad by měl být správně, ale nevím právě, jak zjistit ty kořeny v obloukové míře.
Děkuji za rady.

byk7 · 19. 03. 2013 18:46

http://wiki.matweb.cz/index.php/Rovnice … qrt%282%29

MirekH · 19. 03. 2013 18:47 — Editoval MirekH (19. 03. 2013 18:48)

Tvůj výsledek je správný, ale do radiánů ho budeš muset nejspíš přepočítat na kalkulačce.

Nicméně existuje podstatně jednodušší způsob řešení. Nejprve celou rovnici vydělíš dvěma
$\frac{1}{2}\sin x + \frac{\sqrt{3}}{2}\cos x = \frac{\sqrt{2}}{2}$ ,
což se dá napsat pro $y = \frac{\pi}{3}$ jako
$\sin(x + y) = \sin x \cos y + \cos x \sin y$ ,
tedy
$\sin$x + \frac{\pi}{3}$ = \frac{\sqrt{2}}{2}$ .
Najít hodnotu x je potom hračka.

zdenek1 · 19. 03. 2013 18:49

↑ bejf:
$\sin x+\sqrt{3}\cos x=\sqrt{2}\qquad :2$
$\frac12\sin x+\frac{\sqrt{3}}2\cos x=\frac{\sqrt{2}}2$
$\cos x\cos \frac\pi6+\sin x\sin\frac\pi6=\frac{\sqrt{2}}2$
$\cos \left(x- \frac\pi6\right)=\frac{\sqrt{2}}2$
$x-\frac\pi6=\pm\frac\pi4+2k\pi$ , $k\in\mathbb Z$

mukel · 19. 03. 2013 18:49

čiže... y1= \sqrt{2}/2
y2= \sqrt{-4}/2

To druhé riešenie nevyhovuje, keďže takéto číslo nepatrí do množiny R.

Pre to riešenie y1 však vieme nájsť také x, pre ktoré sin(x)= \sqrt{2}/2, urobíme návrat k substitúcii tak, že za y dosadíme prípustné riešenia kvadratickej rovnice.

zdenek1 · 19. 03. 2013 18:54

↑ bejf:
Ten výsledek samozřejmě jde vypočítat bez kakulačky
Stačí si ho přepsat jako $\frac{\sqrt{2}}{2}\cdot \frac{1}{2}\pm\frac{\sqrt2}{2}\cdot \frac{\sqrt3}{2}$
a použít vzorec pro $\cos(x\mp y)$

Hlavní problém u tvé metody je, že musíš udělat zkoušku, protože umocnění je neekvivalentní úprava.

byk7 · 19. 03. 2013 18:58

↑ MirekH:

To není pravda, pokud považujeme hodnoty sin(15°) a sin(75°) za známé ;-)

bejf · 19. 03. 2013 19:04

↑ mukel:↑ zdenek1:↑ MirekH:↑ byk7:
Díky za upozornění. Je mi útěchou, že jsem se k tomu alespoň dobral správně, ikdyž složitě. :-)

Matematické Fórum

#1 19. 03. 2013 18:22 — Editoval bejf (19. 03. 2013 18:25)

Goniometrická rovnice

#2 19. 03. 2013 18:46

Re: Goniometrická rovnice

#3 19. 03. 2013 18:47 — Editoval MirekH (19. 03. 2013 18:48)

Re: Goniometrická rovnice

#4 19. 03. 2013 18:49

Re: Goniometrická rovnice

#5 19. 03. 2013 18:49

Re: Goniometrická rovnice

#6 19. 03. 2013 18:54

Re: Goniometrická rovnice

#7 19. 03. 2013 18:58

Re: Goniometrická rovnice

#8 19. 03. 2013 19:04

Re: Goniometrická rovnice

Zápatí