Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 03. 2013 08:11
výpočet s inflací
Dobrý den,
potřebuji pomoct s tímto příkladem, nějak se v tom již ztrácím a nevím už jak dál.
Mám částku 3775109,69 Kč. Chci vše investovat do firmy.
Zde jsou podmínky:
- počáteční vklad 150000 Kč
- Platit roční poplatek = 1000 Kč první rok, pak zvyšující se ročně o % inflace;
Na jak dlouho (započítávají se pouze celé roky) se může podepsat smlouva, pokud inflace je konstantní a rovná 2% ročně?
Děkuji za infrmaci, jak toto vypočítat.
Offline
#2 20. 03. 2013 09:22 — Editoval Cheop (20. 03. 2013 09:24)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: výpočet s inflací
↑ Ely:
Pokud jsem to dobře pochopil:
První rok odepíšeš 151000 (150000 vklad a 1000 roční poplatek
Na další roky ti zbyde:
3775109-151000 = 3624109
Každý rok budeš dávat roční poplatek 1000 s inflací 2 % = 1020
To ti vydrží na: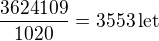
Smlouvu tedy můžeš podepsat na 3554 roků
Nikdo není dokonalý
Offline
#3 20. 03. 2013 09:48 — Editoval Pivňa (20. 03. 2013 09:50)
Re: výpočet s inflací
↑ Cheop:
počítáš s inflací jen na první rok a tak to bohužel nefunguje
vklad 150.000 je jednorázový, stačí ho tedy odečíst 3.775.109,69 - 150.000 = 3.625.109,69
inflace se chová jako geometrická posloupnost. Ze vzorce pro součet prvních n členů geometrické posloupnosti
kde Sn je ta částka, a1 je 1000, q je 1,02 a n je počet let
úpravou výrazu mi vyšlo 217 let.
Offline
