Matematické Fórum

keNN · 20. 03. 2013 09:33

Čau,

když mám příklad

(x+1) (x+4)
(2) + (2) <=51 , tak to udělám podle n!/k!(n-k)! takže x+1/2(x+1-2) + x+4/ 2(x+4-2) <= 51

ale když to rozepíši dál tak mě začne vycházet x v mocninách atd, kde pls chybuji?

Rumburak

Ahoj.
Po tom rozpisu kombinačních čísel do tvaru n!/(k!(n-k)!) (pokud to na levá straně nerovnice je součet dvou kombinačních čísel)
se toho dosti vykrátí a nerovnice tím dostane tvar

$\frac {(x+1)x}{2} + \frac {(x+4)(x+3)}{2}\le 51$ ,

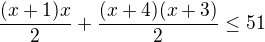což se dá upravit na kvadratickou nerovnici.

byk7 · 20. 03. 2013 09:56

Píšu to už potřetí, prosím, používej závorky!
$&\color{red}n!/k!(n-k)!=\frac{n!}{k!}\cdot(n-k)!=\frac{n!(n-k)!}{k!}\neq\binom{n}{k}=\frac{n!}{k!(n-k)!}=n!/\big(k!(n-k)!\big) \\ &\color{red}x+1/2(x+1-2)+x+4/2(x+4-2)=x+\frac12\cdot(x+1-2)+x+\frac{4}{2}\cdot(x+4-2)=\cdots\neq\binom{x+1}{2}+\binom{x+4}{2}$

Takže k příkladu
$\binom{x+1}{2}+\binom{x+4}{2}&=\frac{(x+1)!}{2!(x-1)!}+\frac{(x+4)!}{2!(x+2)!}=\frac{(x+1)x}{2}+\frac{(x+4)(x+3)}{2}=\frac{$x^2+x$+$x^2+7x+12$}{2}= \\ &=\frac{2x^2+8x+12}{2}=x^2+4x+6$
nerovnice tedy přejde do tvaru
$x^2+4x+6\le51$

Rumburak · 20. 03. 2013 10:13

↑ byk7:
Děkuji za správnou připomínku. Ve svém příspěvku jsem již opravil - holt nepozorné kopírování přes clipboard mívá podobné následky.

byk7 · 20. 03. 2013 12:01

↑ Rumburak: Zdravím, ta moderátorská upomínka samozřejmě nebyla na Tebe, ale na keNNyho, už je to potřetí, co ho napomínám.

keNN · 20. 03. 2013 17:29

diky moc, dam si pozor na tu zavorku

Matematické Fórum

#1 20. 03. 2013 09:33

Kombinatoricka nerovnice

#2 20. 03. 2013 09:54 — Editoval Rumburak (20. 03. 2013 10:10)

Re: Kombinatoricka nerovnice

#3 20. 03. 2013 09:56

Re: Kombinatoricka nerovnice

#4 20. 03. 2013 10:13

Re: Kombinatoricka nerovnice

#5 20. 03. 2013 12:01

Re: Kombinatoricka nerovnice

#6 20. 03. 2013 17:29

Re: Kombinatoricka nerovnice

Zápatí