Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 30. 12. 2008 13:40
Kombinatorika
2.2 Je dán obdélník ABCD a na každé straně je zvoleno 6 vnitřních bodů. Určete počet všech trojúhelníků, jejichž vrcholy E,F,G leží v daných bodech a na různých stranách obdélníku ABCD.
Výsledek je 864,toho sem dosáhl ,ale náhodou a na tu nechci spoléhat.
2.3 Je dán pětiúhelník ABCDE a na každé jeho straně je zvoleno 5 vnitřních bodů. Určete počet všech všech trojúhelníků,jejichž vrcholy X, Y,Z leží v daných bodech a na různých stranách pětiúhelníku. (Výsledek 1 250)
2.6 Určete počet všech trojciferných přirozených čísel, utvořených z číslic 0,1,2,3,4,5 v jejichž dekadickém zápisu se každá vyskytuje nejvýše jednou.
(Výsledek: existuje 100 trojciferných čísel)
2.7
Určete počet všech čtyřciferných přirozených čísel, v jejichž dekadickém zápisu se každá číslice vyskytuje nejvýše jednou. ( existuje 4 536 čtyřciferných přirozených čísel dané vlastnosti)
Offline
#3 30. 12. 2008 14:36
Re: Kombinatorika
↑ Lucas456:
Ahoj .),
těhle příkladů jsou tu spousty, tak přes tlačítko Hledej si jich pár najdi a určitě ti to pomůže (s čím si nebudeš vědět rady, tak se ozvi).
Jinak k tomu poslednímu příkladu (je jednoduchý, tak se nemusím moc rozepisovat ;)): čtyřciferná čísla (nemůžeš začít nulou) bez opakování číslic: 
Offline
#6 30. 12. 2008 14:46
Re: Kombinatorika
↑ Lucas456:
Abych ti řekl pravdu, tak se dostanu k výsledku co máš v závorce napsaný, jen si nejsem jistý, jak bych si ospravedlnil ten postup .)
Offline
#8 30. 12. 2008 14:49
Re: Kombinatorika
↑ Lucas456:
Přesně to, dostanu se k výsledkům co máš napsané v závorkách, ale tím postupem si nejsem u toho jednoho příkladu jistý (te první máš tuším správně, ale nedej na mne, když jde o kombinatoriku ;))
Offline
#11 30. 12. 2008 15:01 — Editoval O.o (30. 12. 2008 15:08)
Re: Kombinatorika
↑ Lucas456:
Ta 2.6 je stejná jako 2.7, jednoduše trojciferná čísla nemohou začínat nulou, takže na první místo můžeme zvolit pouze jedno z pěti čísel, na druhé místo už můžeme dosadit i nulu, ale nesmí tam být číslo z prvního místa, proto tam volíme znovu jen pět čísel (z šesti je jedno na prvním místě, tudíž zůstane pět čísel na rozhazování) a nakoenc na třetí místo můžeme volit pouze ze čtyř čísel, tzn: 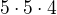
U toho pětiúhelníku vyjde asi opravdu 1250, ale počkej si ještě, co napíše někdo jiný .)
Offline
#14 30. 12. 2008 15:17
Re: Kombinatorika
↑ Lucas456:
Doporučoval bych ti používat tlačítko EDIT, abys neměl za sebou více příspěvků (to je tu preferováno) ;).
Jinak pětiúhelník: 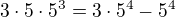
Nebo také takto: 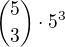
Offline
#15 30. 12. 2008 15:28
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kombinatorika
↑ Lucas456:
Zdravím :-)
obdélník se řešil zde: http://forum.matweb.cz/viewtopic.php?id=3963 a zde: http://forum.matweb.cz/viewtopic.php?id=1264
↑ O.o:
Zdravím srdečně a blahopřeji k Einsteinovi :-)
Offline
