Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 03. 2013 15:18
Goniometrická rovnice
Ahoj, prosím o popostrčení. Mám vyřešit rovnici v R:
Já pak postupoval tak, že jsem si zapsal podmínku  , tedy
, tedy  , převedl zbytek rovnice na společného jmenovatele, a pak jsem se už nedostal nějak dál. Děkuji za rady.
, převedl zbytek rovnice na společného jmenovatele, a pak jsem se už nedostal nějak dál. Děkuji za rady.
Offline
- (téma jako vyřešené označil(a) bejf)
#3 22. 03. 2013 15:47
Re: Goniometrická rovnice
↑ zdenek1:
Jo díky, tak k tomu jsem se dostal taky, ale nevšiml jsem si té kvadratické rovnice. Potom mi to vyjde, ještě navíc teda mi vyjde řešení v  , který ale, pokud správně říkám, je zahrnuto v množině řešení rovnice
, který ale, pokud správně říkám, je zahrnuto v množině řešení rovnice 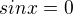 , proto se nezapisuje. Je tak?
, proto se nezapisuje. Je tak?
Offline

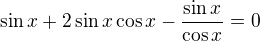

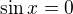 nebo
nebo 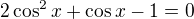 - substituce
- substituce  a vyřešit kv. rci.
a vyřešit kv. rci.