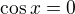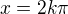Matematické Fórum

bejf · 24. 03. 2013 21:20

No a ještě bych měl jednu chuťovku. Opět se má řešit rovnice v R:
$sinx+sin3x=sin2x+sin4x$
Naznačím svůj postup:
$sinx+sin2x\cdot cosx+cos2x\cdot sinx=2sinx\cdot cosx+2\cdot sin2x\cdot cos2x\nl sinx+2\cdot sinx\cdot cos^2 x+sinx\cdot cos^2 x-sin^3 x=2\cdot sinx\cdot cosx+4\cdot sinx\cdot cosx(cos^2x-sin^2x)\nl sinx+3\cdot sinx\cdot cos^2 x-sin^3 x=2\cdot sinx\cdot cosx+4\cdot sinx\cdot cos^3 x-4sin^3 x\cdot cosx\nl sinx(1-sin^2 x)+3\cdot sinx\cdot cos^2 x=2\cdot sinx\cdot cosx+4\cdot sinx\cdot cos^3 x-4\cdot sin^3 x\cdot cosx\nl 4\cdot sinx\cdot cos^2x=sinx(2\cdot cosx+4\cdot cos^3 x-4\cdot sin^2 x\cdot cosx)\nl 4\cdot cos^2x=2\cdot cosx+4\cdot cos^3 x-4\cdot sin^2 x\cdot cosx\nl 4\cdot cos^2x=2\cdot cosx+4\cdot cos^3 x-4\cdot cosx \cdot (1-cos^2x)\nl 4\cdot cos^2x=2\cdot cosx+4\cdot cos^3 x-4\cdot cosx + 4\cdot cos^3x\nl 8\cdot cos^3 x-4\cdot cos^2x-2\cdot cosx=0\nl 2\cdot cosx(4\cdot cos^2x-2\cdot cosx-1)=0$
Potom jsem zjistil, že:
$2\cdot cosx=0\nl x=\frac{\pi}{2}+k\pi$
a závorku jsem řešil substitucí $cosx=t$
A dál:
$4t^2 -2t-1=0\nl D=20\nl t_{1,2}=\frac{2\pm \sqrt{20}}{8}=\frac{2(1\pm \sqrt{5})}{8}=\frac{1\pm \sqrt{5}}{4}$
No a tady jsem skončil. Chybí mi ještě zjistit dvě řešení. Ale je dost možný, že někde dělám chybu, jen ji nevidím. Děkuji za rady.

Arabela

Ahoj ↑ bejf:,
prečo to nedokončíš?
$\cos x=\frac{1+\sqrt{5}}{4}$
$x'=36^\circ$ , atď. ...
Ja som pri riešení tej rovnice použila vzorce pre súčet gon. funkcií:
$\sin x+\sin 3x=2\sin 2x\cos x$
$\sin 4x+\sin 2x=2\sin 3x\cos x$
Po úpravách
$\cos x(\sin 3x-\sin 2x)=0$ .
Odtiaľ
$\cos x=0$
alebo
$\sin 3x=\sin 2x$

$x=\frac{\pi }{2}+k\pi$
alebo
$x=2k\pi$
alebo
$x=(2k+1)\frac{\pi }{5}$

bejf · 24. 03. 2013 22:06

↑ Arabela:
Dobře, šel jsem na to trochu složitě. :D
Jenom ještě teda nevím, jak se dá zjistit z $cosx=\frac{1+\sqrt{5}}{4}$ že je 36°, kromě toho, že si tu hodnotu vypočítám na kalkulačce a najdu v tabulkách?
A jak poznám z $sin3x=sin2x$ ty poslední dvě řešení, aniž bych si dělal graf?

Arabela · 24. 03. 2013 22:19

↑ bejf:
najskôr k tej druhej otázke. Platí veta
$(\sin \alpha =\sin \beta) \Leftrightarrow \exists k\in Z: \alpha =\beta +2k\pi \vee \alpha =\pi -\beta +2k\pi$
Keď sa tak zamyslíš nad jej obsahom, je vlastne dosť zrejmý - sínusy dvoch uhlov sa rovnajú len vtedy, ak sa rovnajú priamo uhly (až na celočíselné násobky 2 pí), alebo ak jeden z uhlov je doplnkom toho druhého do 180 stupňov (pí), a teda opäť nesmieme zabudnúť na tie násobky...
Toto je zrejmé?

bejf · 24. 03. 2013 22:25

↑ Arabela:
Jasně, chápu.

Arabela · 24. 03. 2013 22:33

↑ bejf:
no a čo sa týka tej prvej otázky, ak nechceš použiť kalkulačku ani tabuľky a chceš mať istotu presného riešenia, môžeš sa obrátiť na nejakých kvalitnejší lexikom matematiky, kde sa uvádzajú presné hodnoty goniometrických funkcií aj nie najbežnejších "významných" uhlov, akými sú napríklad 72 stupňov (=360stupňov/5), resp. 36 stupňov (=360 stupňov/10). K týmto hodnotám je možné sa dopracovať riešením binomických rovníc algebraickým a goniometrickým spôsobom a ich porovnaním)...

MirekH · 24. 03. 2013 22:44

Jestli můžu doplnit, tak existuje takový trikový způsob, jak přijít na těch 36° - stačí si všimnout, že $\frac{1 + \sqrt{5}}{4}$ je polovina zlatého řezu ( $\varphi$ ). A jelikož uhlopříčka a strana v pětiúhelníku jsou v poměru zlatého řezu a svírají spolu úhel 36°, bude $\cos(36°) = \varphi/2$ .

Arabela · 24. 03. 2013 22:55

↑ MirekH:
vďaka za ďalšiu zaujímavú súvislosť...

bejf · 25. 03. 2013 07:25

Dobře, už rozumím. Moc děkuju. :-)

Matematické Fórum

#1 24. 03. 2013 21:20

Goniometrická rovnice

#2 24. 03. 2013 21:41 — Editoval Arabela (24. 03. 2013 21:43)

Re: Goniometrická rovnice

#3 24. 03. 2013 22:06

Re: Goniometrická rovnice

#4 24. 03. 2013 22:19

Re: Goniometrická rovnice

#5 24. 03. 2013 22:25

Re: Goniometrická rovnice

#6 24. 03. 2013 22:33

Re: Goniometrická rovnice

#7 24. 03. 2013 22:44

Re: Goniometrická rovnice

#8 24. 03. 2013 22:55

Re: Goniometrická rovnice

#9 25. 03. 2013 07:25

Re: Goniometrická rovnice

Zápatí