Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » uzavřenost normovaného podprostoru (TOTO TÉMA JE VYŘEŠENÉ)
#1 21. 03. 2013 17:51
uzavřenost normovaného podprostoru
Dobrý den. Mám za úkol ukázat, že každý podprostor konečnědimenzionálního normovaného prostoru je uzavřený. Takže jde vlatně o to ukázat, že u konečně mnoha dimenzí se nemůže stát, že by nějaká posloupnost vykonvergovala ven z prostoru jako je to třeba u prostoru polynomů, které konvergují k e^x. Našel jsem takovou lemmu, podle které každý konečně-dimenzionální prostor je Banachovský, tedy úplný(uzavřený), ale to by taky chtělo důkaz akorát su nejsem jistý, jestli je nutné jít na to touto cestou.
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
- (téma jako vyřešené označil(a) Honza90)
#4 21. 03. 2013 19:25
Re: uzavřenost normovaného podprostoru
↑ Honza90: nějak ti nerozumim. a nechci ti to naservírovat hned celý:)
Offline
#5 21. 03. 2013 22:30
Re: uzavřenost normovaného podprostoru
↑ Stýv:
tak tedy, nechť  je normovaný lineární prostor,
je normovaný lineární prostor,  ,
, 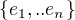 jeho báze.
jeho báze.
Prvek 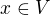 lze vyjádřit jako
lze vyjádřit jako 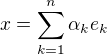 . Definujme normu
. Definujme normu  ,
,  .
.
Zřejmě existuje  takové, že platí nerovnost
takové, že platí nerovnost  pro
pro 
Aby prostor byl úplný(nebo uzavřený..?) musí posloupnost 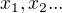 konvergovat k nějakému
konvergovat k nějakému 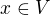 , což nastane právě tehdy, když pro
, což nastane právě tehdy, když pro  ,
, .
.
Dále platí:  z toho plyne, že
z toho plyne, že 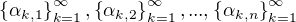 jsou konvergentní posloupnosti.
jsou konvergentní posloupnosti.
Dále pro  máme:
máme: 
Tedy pro 
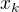 konverguje k
konverguje k 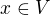 .
.
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#6 22. 03. 2013 11:16 — Editoval Rumburak (22. 03. 2013 11:19)
Re: uzavřenost normovaného podprostoru
↑ Honza90:
Ahoj.
Připadá mi, že jsi správně nepochopil nejen radu, kterou Ti dal ↑ Stýv:, ale ani tu úlohu.
Je dán LN prostor  konečné dimense a jeho podprostor
konečné dimense a jeho podprostor  . Máš dokázat, že
. Máš dokázat, že  je ve
je ve 
uzavřenou množinou, což znamená, že pokud nějaká posloupnost  prvků z
prvků z  má ve
má ve  limitu
limitu  ,
,
potom  .
.
Offline
#7 22. 03. 2013 13:20
Re: uzavřenost normovaného podprostoru
↑ Rumburak:
Tu radu jsem nepochopil. Ano nenapsal jsem tam, ze V je podprostor, ale princip důkazu bude asi stejný, ne?
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#8 22. 03. 2013 15:59 — Editoval Rumburak (22. 03. 2013 16:12)
Re: uzavřenost normovaného podprostoru
Aby prostor byl úplný(nebo uzavřený..?) musí posloupnost
konvergovat k nějakému
, c
Která posloupnost je míněna ? O žádné konkretní se nezmiňuješ a obecně to jistě neplatí, i v úplném prostoru mohou existovat nekonvergentní
posloupnosti, v jeho uzavřeném podprostoru rovněž.
Ta část, která ukazuje, že Cauchyovská posloupnost má limitu (pokud se správně domýšlím, že o takový důkaz Ti šlo - nikde to nepíšeš),
je myšlenkově správně, ale chybí specifikace prvku  , který má být touto limitou.
, který má být touto limitou.
Když pomineme uvedené formální nadostatky, dokázal jsi větu, že každý reálný LN prostor konečné dimense je úplný.
A jak z toho odvodíš, že jeho podprostor je v tom "větším" prostoru kon. dimene uzavřenou množinou ?
I když je to celkem triviální, nelze toto finále důkazu pominout.
EDIT.
Úplnost prostoru je něco jiného než jeho uzavřenost. Mám dojem (již z prvního příspěvku), že máš tendenci je zaměňovat.
Offline
#9 23. 03. 2013 10:08
Re: uzavřenost normovaného podprostoru
↑ Rumburak:
Rozdíl mezi uzavřenosti a úplnosti mi není úplne jasny, tím jsem možna měl začít.
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#10 23. 03. 2013 12:37
Re: uzavřenost normovaného podprostoru
↑ Honza90:
Mějme dejme tomu metrický prostor  .
.
I. Množina 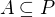 je uzavřená v prostoru
je uzavřená v prostoru  , právě když platí:
, právě když platí:
Je-li  posloupnost prvků množiny
posloupnost prvků množiny  mající v
mající v  limitu
limitu  (tedy limita existuje a patří do množiny
(tedy limita existuje a patří do množiny  ),
),
potom  .
.
Příklady: Prázdná množina a množina  jsou množiny uzavřené v
jsou množiny uzavřené v  .
.
Definice uzavřenosti množiny bývá obvykle pojímána jinak, ale ekvivalentně s výše uvedenou větou.
II. Úplnost metrického prostoru znamená, ža každá cauchyovská posloupnost má v něm limitu.
Platí věta:
Nechť  je úplný metrický prostor,
je úplný metrický prostor,  ,
, 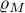 je zúžení metriky
je zúžení metriky  na množinu
na množinu  . Potom
. Potom  je
je
úplný podprostor prostoru  právě tehdy, je-li množina
právě tehdy, je-li množina  uzavřená v
uzavřená v  .
.
Takže V RÁMCI ÚPLNÉHO PROSTORU  splývají pojmy jeho úplného podprostoru a uzavřeného podprostoru,
splývají pojmy jeho úplného podprostoru a uzavřeného podprostoru,
ale obecně tomu tak není.
Offline
#11 23. 03. 2013 23:25
Re: uzavřenost normovaného podprostoru
↑ Rumburak:
Díky moc za vysvětlení. Takze je-li podprostor úplný pak je automaticky také uzavřený, ale může existovat uzavřený, který není úplný. Ale konečně dimenzionalni normované prostory jsou vždy úplné, takže v nich nemůže existovat otevřený podprostor. Dá se s tím souhlasit?
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#12 25. 03. 2013 10:07 — Editoval Rumburak (25. 03. 2013 11:24)
Re: uzavřenost normovaného podprostoru
↑ Honza90:
S těmi pojmy nutno zacházet opatrně.
1) Úplnost PROSTORU (či jeho podprostoru) má absolutní platnost: daný prostor - ať již sám o sobě nebo jako podprostor jiného prostoru -
úplný buďto je nebo není, což závisí pouze na něm samém.
2) S otevřeností či uzavžeností PODMNOŽIN metrického prostoru  je tomu jinak. Zda jeho podmnožina
je tomu jinak. Zda jeho podmnožina  je V NĚM otevřená,
je V NĚM otevřená,
uzavřena, obojetná (=zároveň otevřená i uzavřená), případně ani uzavřená ani otevřená (všechny tyto případy jsou teoreticky možné,
uzvřenost NENÍ negací otevřenosti), obecně závisí též na prostoru  . Hovoříme-li o otevřenosti nebo uzavřenosti množin,
. Hovoříme-li o otevřenosti nebo uzavřenosti množin,
měli bychom vždy uvádět, ke kterému prostoru je vztahujeme.
Příklady:
Podmnožiny  metrického protstoru
metrického protstoru  jsou v něm obojetnými množinami .
jsou v něm obojetnými množinami .
Polouzavřený interval  v prostoru reálných čísel s eukleidovskou metrikou není ani uzavřenou ani otevřenou množinou,
v prostoru reálných čísel s eukleidovskou metrikou není ani uzavřenou ani otevřenou množinou,
ale v metrickém prostoru  , kde
, kde  je příslušné zúžení eukleidovské metriky, je uzavřenou množinou.
je příslušné zúžení eukleidovské metriky, je uzavřenou množinou.
Úvahu
Konečně dimenzionalni normované prostory jsou vždy úplné, takže v nich nemůže existovat otevřený podprostor.
nejspíš mysliš dobře, ale trochu bych ji přeformuloval, stručně dejme tomu takto:
Podprostor Y v LNP X konečné dimense má rovněž konečnou dimensi, proto je úplný, takže Y je množinou uzavřenou v X.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » uzavřenost normovaného podprostoru (TOTO TÉMA JE VYŘEŠENÉ)

