Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Nelineární rovnice (numerické řešení) (TOTO TÉMA JE VYŘEŠENÉ)
#1 25. 03. 2013 13:48 — Editoval johnnyl (25. 03. 2013 13:51)
Nelineární rovnice (numerické řešení)
Zdravím, budu mít asi trochu jiný požadavek než ostatní. Potřeboval bych nějaký pěkný příklad (slovní úlohu) vedoucí na nelineární rovnici, nejlépe takovou, kterou analyticky nelze řešit. Na příkladu chci demonstrovat numerické metody (bisekci, Newtonovu metodu). Nepotřebuji samotné řešení (aspoň doufám), pouze zadání nějakého příkladu z matematiky nebo fyziky. Ideálně takového, který je dobře pochopitelný, nejlépe se "středoškolskou tématikou." Aby to nebylo pouze "určete kořeny rovnice ..."
Např. pro volný pád s odporem vzduchu z výšky 50m platí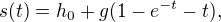
kde  je počáteční výška, takže pokud chceme zjistit čas
je počáteční výška, takže pokud chceme zjistit čas  , kdy těleso dopadne na zem, musíme vyřešit rovnici
, kdy těleso dopadne na zem, musíme vyřešit rovnici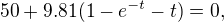
což lze provést pouze numericky.
Podobný příklad znám třeba z analytické geometrie (nejkratší vzdálenost bodu od nějaké křivky).
Offline
- (téma jako vyřešené označil(a) johnnyl)
#2 25. 03. 2013 19:38
Re: Nelineární rovnice (numerické řešení)
↑ johnnyl:
Ahoj,
okamžitě mě napadá, že odpor vzduchu nepůsobí jen při volném pádu, ale třeba i na kmitající pružinu. Výchylka pružiny v odporujícím prostředí je
takže je možné se třeba ptát, ve kterém časovém okamžiku (okamžicích) bude mít pružina výchylku, která se rovná polovině (třetině, dvěma třetinám...) původní amplitudy A_0. Přitom parametry (tlumení alfa, úhlovou frekvenci omega a fázi fí) lze volit tak, že rovnice má prakticky libovolný počet řešení.
Další (dokonce poněkud dobrodružný) příklad by mohl být takový:
Země se pohybuje kolem Slunce po elipse dané rovnicí.... Byla objevena kometa, jejíž dráha je ve stejné rovině jako dráha Země, je hyperbolická o rovnici ... Hrozí srážka se Zemí? A počítejte pozorně - závisí na vás osud lidstva!
To je ovšem trochu náročnější na přípravu (aby to bylo věrohodné). Obě rovnice musejí být v polárním tvaru (Slunce je ve společném ohnisku). Je-li toto ohnisko v pólu souřadné soustavy, je rovnice kuželosečky v polárních souřadnicích 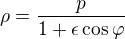 , kde 0<epsilon <1 pro elipsu; epsilon =1 pro parabolu; epsilon>1 pro hyperbolu. Parametry dráhy Země jsou dostatečně známy, pro kometu by se musely vymyslet. Obě rovnice by se musely převést do kartézské souřadné soustavy a hledaly by se průsečíky kuželoseček. A i když se najdou, znamená to jen, že se protnou dráhy těles. K tomu, aby došlo ke srážce, musí být obě tělesa v průsečíku ve stejný okamžik - pak sbohem a šáteček, odcházíme za dinosaury...
, kde 0<epsilon <1 pro elipsu; epsilon =1 pro parabolu; epsilon>1 pro hyperbolu. Parametry dráhy Země jsou dostatečně známy, pro kometu by se musely vymyslet. Obě rovnice by se musely převést do kartézské souřadné soustavy a hledaly by se průsečíky kuželoseček. A i když se najdou, znamená to jen, že se protnou dráhy těles. K tomu, aby došlo ke srážce, musí být obě tělesa v průsečíku ve stejný okamžik - pak sbohem a šáteček, odcházíme za dinosaury...
I tady je to ovšem ještě trochu složitější - aby parametr fungoval skutečně jako čas, museli bychom obě kuželosečky přeparametrizovat tak, aby se líbily panu Keplerovi - aby totiž platil zákon konstantní plošné rychlosti. Ale i to by koneckonců asi šlo udělat.
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#3 25. 03. 2013 22:57
Re: Nelineární rovnice (numerické řešení)
↑ martisek:
Pružinový oscilátor se mi líbí. Uvažoval jsem o něm už dříve, jelikož tento matematický model jsme dost podrobně rozebírali, ale automaticky jsem pokládal  , což je vlastně nalezení času, kdy těleso prochází rovnovážnou polohou. No a tuto rovnici lze snadno analyticky vyřešit. Pokud budu hledat čas, ve kterém je těleso v libovolné nenulové výšce, tak získám takovou rovnici, kterou potřebuji :-) Parametry už si vhodně zvolím.
, což je vlastně nalezení času, kdy těleso prochází rovnovážnou polohou. No a tuto rovnici lze snadno analyticky vyřešit. Pokud budu hledat čas, ve kterém je těleso v libovolné nenulové výšce, tak získám takovou rovnici, kterou potřebuji :-) Parametry už si vhodně zvolím.
Nad druhým příkladem zkusím popřemýšlet, ale zdá se mi dost složitý. Slovní zadání je ale pěkné.
V každém případě děkuji za inspiraci. A kdyby měl někdo ještě další nápad, můžete přispět :-)
Offline
#4 26. 03. 2013 09:43
Re: Nelineární rovnice (numerické řešení)
↑ johnnyl:
To tvé zadání z prvního příspěvku mi přijde dost divné. Ve vzorci 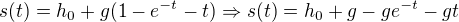 jsou rozměry jednotlivých členů po řadě m,m,ms^-2,??,ms^1. To nejde sčítat. Ty otazníky jsou tam proto, že výraz
jsou rozměry jednotlivých členů po řadě m,m,ms^-2,??,ms^1. To nejde sčítat. Ty otazníky jsou tam proto, že výraz 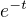 je nesmyslný, všechny matematické funkce musí ve fyzikálních vzorcích mít bezrozměrné argumenty.
je nesmyslný, všechny matematické funkce musí ve fyzikálních vzorcích mít bezrozměrné argumenty.
Kdyby ti nevadila rovnice diferenciální, nabídl bych matematické kyvadlo bez aproximace malých úhlů. Úloha analytické řešení sice má, ale pro běžného smrtelníka který se na to nepřipraví není nalezitelné, a dalo by se pak porovnat jak se liší výsledek od toho aproximovaného výsledku.
Offline
#5 26. 03. 2013 12:41
Re: Nelineární rovnice (numerické řešení)
↑ LukasM:
No nejprve bych opravil ve svém původním příspěvku 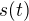 za
za 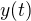 , jelikož se nejedná o vztah pro dráhu, ale okamžitou výšku. Přesný vztah vypadá takto:
, jelikož se nejedná o vztah pro dráhu, ale okamžitou výšku. Přesný vztah vypadá takto: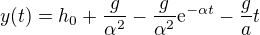
kde  je konstanta. Nevím, jestli má nějaký rozměr, ale pokládal jsem ji rovnu 1.
je konstanta. Nevím, jestli má nějaký rozměr, ale pokládal jsem ji rovnu 1.
Jinak tento vztah jsme odvozovali přímo ve škole a nemyslím, že by na něm bylo něco špatně. Jo a konkrétně výraz 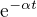 se vyskytuje "v součtu" ve více vztazích, především u volného pádu nebo tělesa na pružině. Nevím, jestli
se vyskytuje "v součtu" ve více vztazích, především u volného pádu nebo tělesa na pružině. Nevím, jestli  "navíc" něco mění.
"navíc" něco mění.
Jinak diferenciální rovnice by mi bohužel vadila, jelikož jejich numerickým řešením jsme se zatím nezabývali :-(
V každém případě děkuji za příspěvek.
Offline
#6 26. 03. 2013 12:52
Re: Nelineární rovnice (numerické řešení)
↑ johnnyl:
Napadá mě ještě toto:
Mezi dva body A, B ve stejné výšce na dvou svislých skalních stěnách má být zavěšena řetězová lávka o délce L (samozřejmě L > |AB|). Vypočtěte prověšení prázdné lávky (tj. o kolik metrů bude nejnižší bod lávky níž než body A;B.)
Řetězovka je pěkná transcendentní křivka, její rovnici, jakož i délku jejího oblouku lze snadno vygooglovat.
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#7 26. 03. 2013 13:33 — Editoval martisek (26. 03. 2013 13:33)
Re: Nelineární rovnice (numerické řešení)
↑ johnnyl:
↑ LukasM: měl pravdu, rozměrově to nesedělo - sečítal jsi dráhu rychlost a zrychlení, což je nesmysl. Je to něco podobného, jako kdybys napsal s = v s tím, že čas tam být nemusí, protože je roven jedné. To je nesmysl - čas nemůže být roven jedné, ale jedné sekundě (která tam bez toho času chybí). To  , i když je číselně rovno jedné, tam z tohoto důvodu být musí taky. Z toho vzorce je teď vidět, že má rozměr sekunda na mínus první a vzoreček už je rozměrově v pořádku.
, i když je číselně rovno jedné, tam z tohoto důvodu být musí taky. Z toho vzorce je teď vidět, že má rozměr sekunda na mínus první a vzoreček už je rozměrově v pořádku.
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#8 26. 03. 2013 15:45
Re: Nelineární rovnice (numerické řešení)
↑ martisek:
Nejsem si zcela jistý, jestli správně chápu tento problém. S řetězovkou jsem se už setkal, na wikipedii jsem teď našel potřebné vztahy, akorát mě trochu mate parametr  a nevím, zda je základním problémem tohoto příkladu zjištění konkrétní hodnoty parametru
a nevím, zda je základním problémem tohoto příkladu zjištění konkrétní hodnoty parametru  .
.
V každém případě, pokud znám |AB|, tak se mi zdá, že stačí spočítat funkční hodnotu f(|AB|/2) a f(0) a jejich rozdíl je poté prověšení lávky.
Offline
#9 26. 03. 2013 19:09 — Editoval martisek (26. 03. 2013 22:20)
Re: Nelineární rovnice (numerické řešení)
↑ johnnyl:
Problém je následující: Řetězovka má rovnici 

x známe - |AB|/2; ale neznáme a. Řetězovka prochází bodem ![kopírovat do textarea $\[ \frac {|AB|} 2 ; y \]$](/mathtex/9a/9a854cf430165023fa8dd72c11e0eaf5.gif) , ale neznáme y. Délka oblouku řetězovky mezi body S; A je
, ale neznáme y. Délka oblouku řetězovky mezi body S; A je
L známe (délka lávky), x známe - |AB|/2. Jádro problému je tedy opravdu ve výpočtu a (ze druhé rovnice). To ale ještě není prověšení - je třeba dosadit do první rovnice a spočítat y. Prověšení je pak y-a.
Hezké na té úloze je to, že se nemusí moc přemýšlet nad tím, jak zadat AB a délku lávky. Stačí si představit si nějaký široký a hluboký kaňon (pár takových "lávek" jsem ve filmech viděl a studenti určitě taky) a délku lávky dát o pěkných pár metrů větší (možná i desítek metrů - jinak by se ji nemuselo podařit natáhnout). No a počítejme....
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#10 26. 03. 2013 22:03
Re: Nelineární rovnice (numerické řešení)
↑ martisek:
Děkuji za detailní vysvětlení. Parametr  asi lze opravdu spočítat pouze numericky. Měl bych ovšem ještě dotaz ke vztahu pro délku oblouku - na wikipedii je vztah
asi lze opravdu spočítat pouze numericky. Měl bych ovšem ještě dotaz ke vztahu pro délku oblouku - na wikipedii je vztah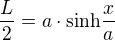 ,
,
takže by mě zajímalo, jestli náhodou nemá být ve vztahu, který uvádíte, znaménko - místo +. Zkoušel jsem jej i odvodit a měl by být správně.
Offline
#11 26. 03. 2013 22:20
Re: Nelineární rovnice (numerické řešení)
↑ johnnyl:
Jasně - to byl omyl (zkopíroval jsem vzoreček a nedostatečně jsem přepisoval :-) Už je opraveno.
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#12 26. 03. 2013 22:57
Re: Nelineární rovnice (numerické řešení)
↑ martisek:↑ martisek:
V pořádku :-) Vhodné parametry v zadání už si zvolím. Tato úloha se mi rovněž líbí a ještě jednou tedy děkuji za inspiraci.
Offline
#13 27. 03. 2013 07:16
Re: Nelineární rovnice (numerické řešení)
↑ johnnyl:
Nebo klasická úloha o koze a paloučku.
Máme travnatý lesní palouk kruhového tvaru o poloměru r. Na okraj lesa uvážeme kozu.
Otázka zní, na jak dlouhém provazu (označme jeho délku např. R) musí být koza uvázaná, aby spásla polovinu plochy palouku.
Řešení: (s využitím plochy kruhové úseče)
Označíme-li 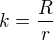 pak musíme vyřešit rovnici.
pak musíme vyřešit rovnici.
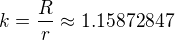
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Nelineární rovnice (numerické řešení) (TOTO TÉMA JE VYŘEŠENÉ)
