Matematické Fórum

Pavel Brožek · 28. 03. 2013 14:40

Přemýšlím, jak by bylo možné rozdělit povrch koule na $n$ shodných částí. Je zřejmé, že to je možné pro libovolné přirozené $n$ (kouli rozdělíme $n$ poledníky). Ale jak to udělat, aby části byly co "nejkompaktnější" (abych to formuloval přesněji, tak chceme co nejmenší vzdálenost $x$ dvou nejvzdálenějších bodů jedné části)? Pro $n\in\{4,6,8,12,20\}$ toho asi dosáhneme promítnutím hran pravidelného mnohostěnu na povrch koule. 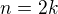Pro sudá $n=2k$ pak ještě můžeme povrch rozdělit rovníkem a $k$ poledníky. Je ale nějaká možnost pro jiná $n$ tak, aby $x<2r$ pro lichá $n$ resp. $x<\sqrt2 r$ pro sudá $n$ , kde $r$ je poloměr koule?

Výsledky:

Pavel Brožek

Ještě mě teď napadlo, že bychom mohli vzít platónské těleso a pro každou jeho stěnu najít její střed a nakreslit z něj úsečky k vrcholů stěny a středům hran stěny, tím bychom dostali další dělení povrchu koule po promítnutí.

Pavel Brožek · 28. 03. 2013 14:58

Tak to není tak jednoduché :D

http://cs.stmarys.ca/~dawson/images4.html#SuperIcos
http://www.math.sci.hiroshima-u.ac.jp/h … 63-540.PDF

Matematické Fórum

#1 28. 03. 2013 14:40

Dělení povrchu koule na shodné díly

#2 28. 03. 2013 14:48 — Editoval Pavel Brožek (28. 03. 2013 14:49)

Re: Dělení povrchu koule na shodné díly

#3 28. 03. 2013 14:58

Re: Dělení povrchu koule na shodné díly

Zápatí