Matematické Fórum

xxxxx19

Ahoj, řeším rovnici:
$y''-2y'+y=0$
v oboru komplexních čísel, ale následující problém je stejný i pro reálné.

mám najít řešení pomocí obecné řady $\sum_{n=0}^{\infty }a_{n}x^{n}$ , hledám tedy koeficienty $a_{n}$

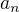
zatím sem se dobral k rekurentnímu vztahu:
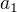$a_{n}=\frac{2}{n}a_{n-1}-\frac{a_{n-2}}{n(n-1)}$ pro $n>2$ nebot $a_{0}$ , $a_{1}$ jsou dvě počáteční podmínky pro rovnici druhého řádu

a nyní nvm jak toto generalizovat na sumu, rozepsat se mi nepovadlo.

Díky za pomoc.

pietro · 30. 03. 2013 23:52

↑ xxxxx19: ahoj, a takto by to nešlo?

http://www.wolframalpha.com/input/?i=a% … 281%29%3Dv

Brano · 31. 03. 2013 00:56 — Editoval Brano (31. 03. 2013 00:57)

↑ xxxxx19:
kedze vies ake riesenia ma ta rovnica, tak vies ako asi budu $a_n$ vyzerat a potom si mozes akoze "tipnut" ze
skumame $b_n=n!a_n$ a dostanes rovnicu
$b_n=2b_{n-1}-b_{n-2}$ a tu uz asi zvladnes vyriesit - vyjde
$b_n=pn+q=(b_1-b_0)n+b_0$

Matematické Fórum

#1 23. 03. 2013 12:10 — Editoval xxxxx19 (23. 03. 2013 12:12)

Diferenciální rovnice

#2 30. 03. 2013 23:52

Re: Diferenciální rovnice

#3 31. 03. 2013 00:56 — Editoval Brano (31. 03. 2013 00:57)

Re: Diferenciální rovnice

Zápatí