Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 31. 03. 2013 13:34
Úprava goniometrickým výrazů
Dobrý den, potřeboval bych vysvětlit(popřípadě i s vyřešením) úpravy 2 goniomet. výrazů:
1, 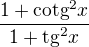 u tohoto příkladu vím, že musím cotg i tg převést na cos/sin a sin/cos a následně je roznásobit, problém mi spíš dělají 1čky
u tohoto příkladu vím, že musím cotg i tg převést na cos/sin a sin/cos a následně je roznásobit, problém mi spíš dělají 1čky
2,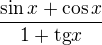 - u tohoto zase nevím co udělat s sinx+cosx(možná použít vzorec
- u tohoto zase nevím co udělat s sinx+cosx(možná použít vzorec  , a následně i znovu co s tou 1čkou =D
, a následně i znovu co s tou 1čkou =D
Předem děkuji
Offline
- (téma jako vyřešené označil(a) Kaney)
#2 31. 03. 2013 13:35 — Editoval Blackflower (31. 03. 2013 13:38)
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Úprava goniometrickým výrazů
↑ Kaney: 1. využi  , pekne sa to pokráti
, pekne sa to pokráti
Offline
#4 31. 03. 2013 13:40 — Editoval Blackflower (31. 03. 2013 13:54)
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Úprava goniometrickým výrazů
↑ Kaney: 2. napíš si tangens ako podiel sínusu a kosínusu a uprav zlomok v menovateli na spoločný menovateľ
Offline
#6 31. 03. 2013 14:27 — Editoval Blackflower (31. 03. 2013 14:29)
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Úprava goniometrickým výrazů
↑ Kaney: Mne to vychádza takto:
1. 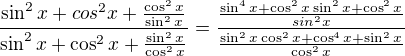
Teraz si v čitateli a menovateli veľkého zlomku pozri členy, ktoré sú rádovo na štvrtú - všetky sú v čitateli menších zlomkov (teda dvojica 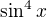 a
a 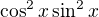 a dvojica
a dvojica 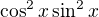 a
a 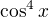 ). Dá sa tam niečo vyňať a tak sa ti riadok, kde tieto dvojice boli, zredukuje na
). Dá sa tam niečo vyňať a tak sa ti riadok, kde tieto dvojice boli, zredukuje na 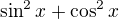 .
.
Dúfam, že je to zrozumiteľné, lebo takéto veľké zlomky písať v texu je dosť pracné.
Offline
#7 31. 03. 2013 14:28
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Úprava goniometrickým výrazů
↑ Kaney: Čo sa týka dvojky, mám pocit, že by sa tam malo vykrátiť 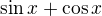 .
.
Offline
#8 31. 03. 2013 14:39
Re: Úprava goniometrickým výrazů
↑ Blackflower:
Proč ten první příklad tak složitě?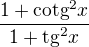
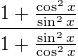
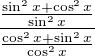
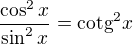
Nezapomeň uvést podmínky ...
Offline
#9 31. 03. 2013 14:44
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Úprava goniometrickým výrazů
↑ ChMcL: Prvý raz som to robila takto... potom mi asi preplo... toto je samozrejme jednoduchšie a zrozumiteľnejšie.
Offline

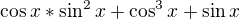 a to je konečná?
a to je konečná?