Matematické Fórum

Blackflower

Zdravím všetkých matematikov,
vedel by mi niekto poradiť, ako rozvinúť do Fourierovho radu túto funkciu? $f(x)=\cos^3x-3\cos x \sin^2x$
My zapisujeme Fourierov rad v takomto tvare: $\frac{a_0}{2}+\sum_{n=1}^{\infty}a_n\cdot \cos nx+\sum_{n=1}^{\infty}b_n\cdot \sin nx$
Podarilo sa mi zistiť, že funkcia je párna, takže koeficienty 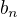$b_n$ budú nulové. Podarilo sa mi vypočítať $a_0$ (aj keď neviem, či je dobre):
$a_0=\frac{1}{\pi }\int_{-\pi}^{\pi}f(x)\mathrm{d}x$ - vyšlo nula
Mám problém s $a_n$ :
$a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cdot\cos nx=\frac{1}{\pi}\int_{-\pi}^{\pi}(\cos^3x-3\cos x \sin^2x)\cdot\cos nx$
Pokúsila som sa funkciu nejako si upraviť; ďalší tvar, čo mi vyšiel, bol $4\cos^3x-3\cos x$ . Skúšala som integrovať obidve tieto veci, ale vždy som sa zamotala.

Vedel by niekto, čo s tým? Nechcem od nikoho, aby to počítal namiesto mňa, len keby mi niekto napríklad vedel poradiť, ktorý z tých tvarov je lepšie integrovať a pod. Taktiež by som určite využila aj nejaké triky k výpočtu koeficientov radov, keďže per partes mi zatiaľ moc nepomohlo, len som sa zacyklila.

(Z Moivrovej vety mi vyšiel rozvoj veľmi jednoducho - $\cos 3x$ , ale neviem, či je to dobre).

Budem vďačná za každú pomoc.

Brano · 31. 03. 2013 16:05 — Editoval Brano (31. 03. 2013 16:06)

ak si zvladla
$\cos 3x=\cos^3x-3\cos x\sin^2 x$
tak to uz mas snad hotovo ...
vzorec
$\frac{1}{\pi}\int_{-\pi}^\pi\cos mx\cos nx=\delta_{mn}$
poznas nie?

alebo inymi slovami ... rozlozit $\cos 3x$ do radu $a_n\cos nx$ je trivialne
$a_3=1$ a pre $n\not=3$ je $a_n=0$

Blackflower

↑ Brano: To je v podstate "súčtový vzorec" pre cos 3x?
Mne to cos 3x vyšlo z Moivreovej vety, to už na rad rozložiť viem, nevedela som, či som to spočítala dobre (z vety).

Brano · 31. 03. 2013 16:10

↑ Blackflower:
urcite sa to da robit vela sposobmi - ja som sa spytal W|A ;-)
rozpisat $\cos 3x$ asi nie je take tazke, ale ako na to prist naopak tak to mi teraz nenapada, ale prisla si na to a to je dolezite

Blackflower · 31. 03. 2013 16:14

↑ Brano: Z tej Moivrovej vety to ide pomerne jednoducho, ale neviem tam urobiť hocičo (aj keď sa to asi dá).

Matematické Fórum

#1 31. 03. 2013 15:21 — Editoval Blackflower (31. 03. 2013 15:21)

Fourierov rozvoj

#2 31. 03. 2013 16:05 — Editoval Brano (31. 03. 2013 16:06)

Re: Fourierov rozvoj

#3 31. 03. 2013 16:06 — Editoval Blackflower (31. 03. 2013 16:09)

Re: Fourierov rozvoj

#4 31. 03. 2013 16:10

Re: Fourierov rozvoj

#5 31. 03. 2013 16:14

Re: Fourierov rozvoj

Zápatí