Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Metrické úlohy. Odchylka přímky od roviny (TOTO TÉMA JE VYŘEŠENÉ)
#1 31. 03. 2013 11:37
Metrické úlohy. Odchylka přímky od roviny
Zadání zní: Je dána krychle ABCDEFGH. Určete odchylku přímky p=CE od roviny 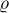 =BDM, kde bod M je střed hrany CG. To je poslední příklad kterej nevím...V těch roviinách to moc nevidím. Prosím o pomoc, jestli víte.
=BDM, kde bod M je střed hrany CG. To je poslední příklad kterej nevím...V těch roviinách to moc nevidím. Prosím o pomoc, jestli víte.
Offline
- (téma jako vyřešené označil(a) luscinka1)
#2 31. 03. 2013 12:27
Re: Metrické úlohy. Odchylka přímky od roviny
↑ luscinka1:
zkus vypočítat úhel pomocí vzorečku 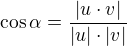 . za
. za  si dosaď vektor, který určuje přímku CE a
si dosaď vektor, který určuje přímku CE a 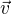 bude vektor ležící v rovině BDM, který leží s vektorem
bude vektor ležící v rovině BDM, který leží s vektorem  v jedné rovině.
v jedné rovině.
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#3 31. 03. 2013 12:29
Re: Metrické úlohy. Odchylka přímky od roviny
No takto sem to dělala, ale tuto úlohu máme řešit pomocí znalostí o geometrii a podobně. Toto jsem měla a učitelka, že to nelze. Máme to vyřešit graficky a početně. A to početně pomocí znalostí co víme. Jako cosinové věty, hledání pravoúhlého trojuhelníku a tak :/
Offline
#4 31. 03. 2013 13:02
Re: Metrické úlohy. Odchylka přímky od roviny
↑ luscinka1:
taky to tak jde, ale není to teda jednodušší. musíš najít průsečík té přímky a roviny a najít, kde v jeho blízkosti svírají rovnoramenný trojúhelník. Napovím, že výška toho průsečíku je 1/4 délky strany krychle.
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#6 31. 03. 2013 15:30
Re: Metrické úlohy. Odchylka přímky od roviny
Ahoj ↑ luscinka1:,
výsledok má byť 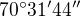 ?
?
server.gphmi.sk/~domanyov
Offline
#8 31. 03. 2013 16:02 — Editoval Honza90 (31. 03. 2013 16:02)
Re: Metrické úlohy. Odchylka přímky od roviny
použijeme analytickou geometrii. osa x vede body A,C, osa y vede body E,A. Délka hrany krychle je 1, délka úhlopříčky je 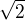 . Rovnice přímky má tvar
. Rovnice přímky má tvar  , určíme rovnici té přímky EC dosazením bodů:
, určíme rovnici té přímky EC dosazením bodů:
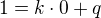
z toho plyne: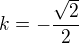
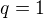
rovnice přímky EC je tedy 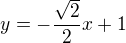
Nyní určíme rovnici přímky představující rovinu BDM: bod x=
bod x=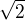 , y=
, y= je bod M, kde rovina protíná hranu krychle
je bod M, kde rovina protíná hranu krychle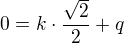 bod x=
bod x=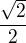 , y=0 je místo, kde rovina protíná spodní stěnu krychle
, y=0 je místo, kde rovina protíná spodní stěnu krychle
rovnice přímky ležící v rovině BDM, která svírá s přímkou EC hledaný úhel je: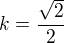 ,
,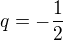

Mimochodem je teď vidět, že sklon přímek je stejný.
Průsečík přimek určíme, tak, že je položíme do rovnosti: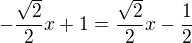
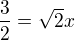
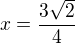
y-ovou souřadnici průsečíku určíme dosazením za x do libovolné rovnice: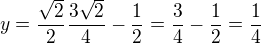
průsečík ![kopírovat do textarea $P=[\frac{3\sqrt{2}}{4},\frac{1}{4}]$](/mathtex/32/3269bdc8225ccd0569671548c2adfb96.gif) a body C a M tvoří rovnoramenný trojúhelník, ve kterém se dá použít pythagorova věta nebo kosinová věta.
a body C a M tvoří rovnoramenný trojúhelník, ve kterém se dá použít pythagorova věta nebo kosinová věta.
Je to takhle lepší, než přes skalární součin? :D
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#9 31. 03. 2013 16:02 — Editoval Arabela (31. 03. 2013 16:05)
Re: Metrické úlohy. Odchylka přímky od roviny
↑ luscinka1:
ja som to riešila nasledovne. Predstav si rovinu ACG (uhlopriečnu rovinu, ktorá rozdelí kocku na dve rovnaké časti). Táto rovina obsahuje priamku EC a "reže" rovinu DBM v priamke S'M, kde S' je stred stenovej uhlopriečky DB. S'M je kolmým priemetom priamky EC do roviny DBM, a teda uhol priamky EC s rovinou DBM je vlastne uhol priamky EC s priamkou S'M. Priesečník týchto dvoch priamok si označme P. Uvažujme ešte stred S telesovej uhlopriečky EC (stred kocky). Máme vypočítať veľkosť uhla S'PS =  . Vypočítame ju nepriamo, pomocou veľkosti uhla
. Vypočítame ju nepriamo, pomocou veľkosti uhla  pri základni rovnoramenného trojuholníka SS'P.
pri základni rovnoramenného trojuholníka SS'P.
Uhol S'SP = uhol S'SCa jeho veľkosť ľahko vypočítame pomocou funkcie tangens (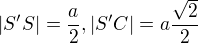 )
)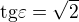
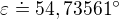
Podobne odvodíme veľkosť druhého uhla pri základni.
Hľadaný uhol 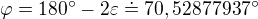
server.gphmi.sk/~domanyov
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Metrické úlohy. Odchylka přímky od roviny (TOTO TÉMA JE VYŘEŠENÉ)

