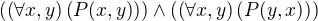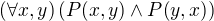Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » postupnosť topológií a sigma-algebier (TOTO TÉMA JE VYŘEŠENÉ)
#1 01. 04. 2013 17:42 — Editoval jarrro (02. 04. 2013 10:37)
postupnosť topológií a sigma-algebier
ahoj napadla ma otázka či môže na reálnych číslach existovať postupnosť množinových systémov kardinality 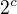 (prípadne nekonečnou ak by to bolo príliš obmedzujúce), ktorá je ostro rastúca v zmysle inklúzie a platí
(prípadne nekonečnou ak by to bolo príliš obmedzujúce), ktorá je ostro rastúca v zmysle inklúzie a platí 
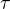 resp.
resp. 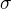 je najmenšia topológia resp. najmenšia sigma-algebra obsahujúca argument
je najmenšia topológia resp. najmenšia sigma-algebra obsahujúca argument
prípadne ešte otázka či by sa zmenila odpoveď keby sa úlohy 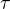 a
a 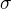 vymenili teda začalo by sa topológiou a pokračovalo sigma-algebrou, teda by sa vymenila párnosť a nepárnosť n v príslušnej rekurzívnej definícii
vymenili teda začalo by sa topológiou a pokračovalo sigma-algebrou, teda by sa vymenila párnosť a nepárnosť n v príslušnej rekurzívnej definícii
MATH IS THE BEST!!!
Offline
- (téma jako vyřešené označil(a) jarrro)
#2 01. 04. 2013 17:48 Příspěvek uživatele Brano byl skryt uživatelem Brano. Důvod: nevsimol som si ze v OP je uz odpoved na moju otazku
#3 01. 04. 2013 17:57 — Editoval Brano (01. 04. 2013 18:09)
Re: postupnosť topológií a sigma-algebier
Len kratke pozorovanie - akonahle je jedna z tych topologii  potom z nej vyrobena
potom z nej vyrobena 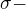 algebra obsahuje jednoprvkove mnoziny a z nej vyrobena topologia obsahuje vsetky mnoziny.
algebra obsahuje jednoprvkove mnoziny a z nej vyrobena topologia obsahuje vsetky mnoziny.
A tiez ze z 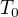 topologie po dvoch krokoch vyrobis
topologie po dvoch krokoch vyrobis  topologiu.
topologiu.
A urcite sa odpoved nezmeni ak zacnes topologiou, lebo ked mas postupnost zacinajucu 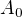 tak mozes zacat od
tak mozes zacat od 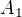 , nech uz
, nech uz 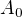 bola topologia ci sigma algebra.
bola topologia ci sigma algebra.
Offline
#4 01. 04. 2013 18:07 — Editoval jarrro (01. 04. 2013 18:09)
Re: postupnosť topológií a sigma-algebier
↑ Brano:díky ak  znamená topológia obsahujúca všetky intervaly tak o tom viem presne tak začalo moje uvažovanie nad danou otázkou.
znamená topológia obsahujúca všetky intervaly tak o tom viem presne tak začalo moje uvažovanie nad danou otázkou.
aha asi to bude topológia spĺňajúca určité oddeľovacie axiómy tak o tom som neuvažoval díky za postreh
MATH IS THE BEST!!!
Offline
#5 01. 04. 2013 18:15 — Editoval Brano (01. 04. 2013 18:18)
Re: postupnosť topológií a sigma-algebier
 znamena, ze pre lubovolne
znamena, ze pre lubovolne 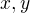 existuje otvorena
existuje otvorena  taka, ze
taka, ze 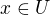 a
a 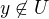 - resp. ekvivalentne, ze jednobodove mnoziny su uzavrete.
- resp. ekvivalentne, ze jednobodove mnoziny su uzavrete.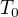 znamena, ze pre lubovolne
znamena, ze pre lubovolne 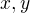 existuje otvorena
existuje otvorena  taka, ze
taka, ze 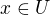 a
a 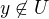 alebo
alebo 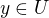 a
a 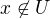 .
.
Napr. topologia generovana  je
je 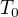 a nie
a nie  .
.
Zvacsa topologie co nie su aspon  su pre topologov nezaujimave. Cize ak taka postupnost existuje, tak bude prudko hnusna.
su pre topologov nezaujimave. Cize ak taka postupnost existuje, tak bude prudko hnusna.
Offline
#6 01. 04. 2013 18:22 — Editoval jarrro (01. 04. 2013 18:23)
Re: postupnosť topológií a sigma-algebier
↑ Brano:díky hneď ako som to dopísal mi došlo, že asi  topológia je topológia v
topológia je topológia v  priestore
priestore
ale nemala by ešte existovať aj otvorená  kde je to naopak? ako to píšu tu?http://mathworld.wolfram.com/T1-SeparationAxiom.html
kde je to naopak? ako to píšu tu?http://mathworld.wolfram.com/T1-SeparationAxiom.html
MATH IS THE BEST!!!
Offline
#10 01. 04. 2013 20:56
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: postupnosť topológií a sigma-algebier
Ahoj,
Otazku bych rozdelil na dve casti:
1) existuje na R vubec nejaka takova ostre rostouci "sigma-tau" posloupnost?
2) musi pak takova posloupnost dosahnout (ve smyslu onoho sjednoceni) az na P(R)?
Predpikladejme, ze odpoved na otazku 1) je kladna. Pak lze misto celeho R uvazovat pouze interval [0,1] (protoze ma mohutnost R a pojmy sigma algebry a topologie jsiu ciste mnozinove, lze tedy priklad na R prenest na [0,1] vhodnou bijekci). Pak polozme![kopírovat do textarea $A:=P([0,1]) \cup \{R\setminus M| M\in P([0,1])\}$](/mathtex/ec/ec4649277225586560851dbf2d7a7c58.gif)
- lze overit, ze toto je sigma algebra i topologie na R.
Necht 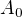 je priklad splnujici pozadavek 1) na mnozine [0,1] (namisto R). Pak staci polozit
je priklad splnujici pozadavek 1) na mnozine [0,1] (namisto R). Pak staci polozit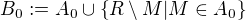
Pak bude posloupnost, zacinajici B_0, take ostre rust. Pritom ale uzaverove operace tau a sigma jsou monotonni a B_0 je podmnozinou A, ktera je jak topologie, tak sigma algebra. Tedy posloupnost Bk nikdy nepreroste A, tedy urcite nedoroste k P(R).
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#11 02. 04. 2013 02:15 — Editoval Brano (02. 04. 2013 02:23)
Re: postupnosť topológií a sigma-algebier
No tak si myslim, ze odpoved je, ze sa to neda. Najprv znacenie. je lubovolna mnozina;
je lubovolna mnozina; 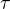 je topologia na
je topologia na  ;
; 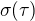 je najmensia sigma-algebra obsahujuca
je najmensia sigma-algebra obsahujuca 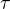 ;
; 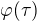 je najmensia topologia obsahujuca
je najmensia topologia obsahujuca 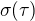 ;
; 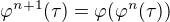 .
.
Vsimnime si, ze 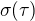 obsahuje vsetky
obsahuje vsetky 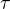 uzavrete mnoziny.
uzavrete mnoziny.
Tvrdenie 1) Ak 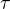 je
je 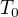 potom
potom 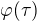 je
je 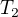
Dokaz: Kedze 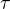 je
je  , tak pre lubovolne
, tak pre lubovolne 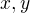 exisuje
exisuje 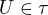 take, ze bud
take, ze bud  alebo naopak. Avsak
alebo naopak. Avsak 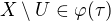 a ta je teda
a ta je teda 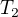 .
.
Tvrdenie 2) Ak 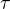 je
je  potom
potom 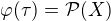
Dokaz: Lubovolna 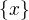 je
je 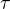 uzavreta a teda
uzavreta a teda 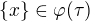 a ta je teda diskretna.
a ta je teda diskretna.
Ako dosledok mame:
Tvrdenie 3) Ak 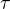 je
je 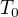 potom pre
potom pre 
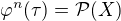
Definujme relaciu  .
.  prave vtedy ked su topologicky nerozlisitelne t.j.
prave vtedy ked su topologicky nerozlisitelne t.j.  . Lahko sa overi, ze je to relacia ekvivalencie na
. Lahko sa overi, ze je to relacia ekvivalencie na  . Triedu ekvivalencie
. Triedu ekvivalencie  oznacme ako standardne
oznacme ako standardne ![kopírovat do textarea $[x]$](/mathtex/21/21271f70d45cc2a593fb2a4b47a16998.gif) a faktorpriestor
a faktorpriestor ![kopírovat do textarea $X/\mathord\sim=\{[x];x\in X\}$](/mathtex/03/031aadbef0841276c5b28022aa71176c.gif) .
.
Na 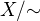 sa definuje faktorova topologia.
sa definuje faktorova topologia. 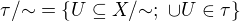 . V tomto pripade sme definovali tzv. Kolmogorov kvocient. Lahko sa nahliadne, ze
. V tomto pripade sme definovali tzv. Kolmogorov kvocient. Lahko sa nahliadne, ze  je
je 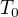 a ze
a ze 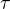 sa da (v tomto pripade) jednoznacne zrekonstruovat z
sa da (v tomto pripade) jednoznacne zrekonstruovat z  t.j.
t.j. 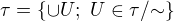 . Operaciu rekonstrukcie oznacme trebars
. Operaciu rekonstrukcie oznacme trebars 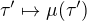
Tvrdenie 4) 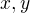 su
su 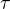 nerozlisitelne prave vtedy ked su
nerozlisitelne prave vtedy ked su 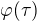 nerozlisitelne.
nerozlisitelne.
Dokaz: Staci si uvedomit, ze pridanie komplementov nerozlisitelnost nepokazi, ani pridanie zjedniteni a ani konecne opakovania tychto dvoch.
To vsak znamena, ze  aj
aj 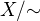 zostavaju rovnake pri prechode od
zostavaju rovnake pri prechode od 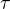 k
k 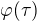 . A tiez ptati:
. A tiez ptati: 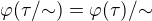 , alebo ekvivalentne.
, alebo ekvivalentne.
Tvrdenie 5) 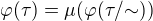
A ked to dame vsetko dohromady, tak dostaneme
Tvrdenie 6) Pre  je
je 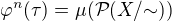 .
.
A teda ta povodna postupnost je najneskor od 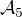 konstantna, ale nemusi byt cele
konstantna, ale nemusi byt cele 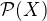 .
.
Offline
#12 02. 04. 2013 10:28 — Editoval jarrro (02. 04. 2013 10:31)
Re: postupnosť topológií a sigma-algebier
díky za vyčerpávajúcu odpoveď aj za odvedenie od omylu ja som si konjunkciu pomýlil s alternatívou pri konjunkcii platí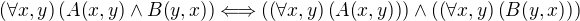
neplatí to pre alternatívu sorry za moju blbosť
MATH IS THE BEST!!!
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » postupnosť topológií a sigma-algebier (TOTO TÉMA JE VYŘEŠENÉ)
 a
a  a tiez musi existovat ...
a tiez musi existovat ...