Matematické Fórum

DragonX · 31. 12. 2008 00:06

Ahoj chtěl bych se zeptat na jeden příklad. Je to na použití posunutí v konstrukci a vůbec si s ním nevím rady.

Zadání: Jsou dány 2 kružnice $k_1(S_1;2,5 cm)$ , $k_2(S_2;3cm)$ , $\left| S_1S_2 \right|=4cm$ a přímka p $\left|S_1p\right|=5cm$ , $\left|S_2p\right|=4cm$ . Sestrojte rovnoběžku s přímkou p, která vytíná na daných kružnicích shodné tětivy.

Ještě jednou připomínám že musí být užito posunutí, což může sloužit jako nějaká nápověda. Děkuji za každou pomoc.

Ivana · 31. 12. 2008 19:40

↑ DragonX:

DragonX

↑ Ivana:
a jak jsi přišla na ty body A a B? a ještě jedný maličkosti nerozumím bod A se do A s čarou ve směru UV přece nepřesouvá?

Ivana · 01. 01. 2009 17:57

↑ DragonX: Koncové body vektoru $UV$ jsem posunula po čárkovaných přímkách až do místa, kde tyto přímky protínají kružnici $k_1$ .... já to ještě předělám a pošlu skenem asi máš pravdu, zkusím to opravit.:-)

DragonX · 01. 01. 2009 18:03

↑ Ivana:
no mně právě není tak docela jasný jak jsi se dostala k těm čárkovaným přímkám... na geometrii moc nejsem to spíš normální počítání :-)

Pavel Brožek · 01. 01. 2009 18:05

↑ DragonX:

Jedná se o příklad 3.113 z učebnice planimetrie pro gymnázia. Řešení z učebnice:

$S_1\in a\perp p,\,A\in p\cap a,\, S_2\in b\perp p,\,B\in p\cap b;$
užijte $T(AB)$

Tak jen doplním, že takto zobrazíš kružnici $k_1$ .

Pavel Brožek · 01. 01. 2009 18:10

↑ Ivana:

Předpokládám, že ses řídila tím 1cm čtverečkováním na papíře. Pak tam máš zřejmou chybu - např. UV určitě není 4cm. Pak také zobrazení T(UV) určitě nezobrazuje body A, B tak, jak píšeš. Popravdě, tvůj postup vlastně ani nechápu a vážně pochybuji o jeho správnosti.

Ivana · 01. 01. 2009 18:30

↑ DragonX:Tak ted´už je to opraveno :

Pavel Brožek · 01. 01. 2009 18:47

↑ Ivana:

Můžeš prosím vysvětlit, proč by měl bod Y', na který se zobrazí bod Y, ležet na kružnici k1 ? A co zaručuje, že opravdu AB=XY ?

Ivana · 01. 01. 2009 18:58

↑ BrozekP:Zdravím v novém roce :-)

Ale bod Y´na kružnici k1 neleží .. ono to asi splývá, ale neleží.
Vzdálenost YY´je právě velikost vektoru UV.

A velikost AB=XY jsou stejně dlouhé...zjistím měřením .

Pavel Brožek · 01. 01. 2009 19:07

↑ Ivana:

Proč tedy bod Y posouváš do bodu Y', když bod Y' nijak nepoužiješ?

"Zjistím měřením" není dobrý důvod. Např. "měřením" na mé kalkulačce jsem zjistil, že Velká Fermatova věta neplatí, protože

$\sqrt[12]{1782^{12}+1841^{12}}=1922$

:-)

Ivana · 01. 01. 2009 19:33

↑ BrozekP:

Znám-li směr a velikost vektoru, pak by mělo pro další konstrukci stačit najít jeden bod. Nebo se mýlím ?

A proč by v planimetrii nemohlo jako důkaz správnosti konstrukce stačit měření konečného sestrojeného výsledku ? (například velikost úhlu, úsečky a pod.)

DragonX · 01. 01. 2009 20:17

↑ Ivana:↑ BrozekP:
díky moc lidi už jsem to dal nějak dohromady ani nevíte jak jste mi pomohli :-)

Ivana · 01. 01. 2009 20:35

↑ DragonX:No nevím ještě budu o tom přemýšlet, ale je to alespoň pro inspiraci :-)

Pavel Brožek · 01. 01. 2009 20:36

↑ Ivana:

Myslíš bod Y, když píšeš o jednom bodě? Já nevím, já té tvé konstrukci moc nerozumím. Proto bych byl rád, kdyby jsi vysvětlila, jak přesně postupovat, když máme dány ty dvě kružnice a přímku p. Jestli jsem nic nepřehlédl, tak jsi ještě ani nenapsala, kde se body U a V vzaly (v zadání nejsou). Člověk si musí domýšlet, jak jsi v konstrukci postupovala, ale mě to celkově nedává smysl.

Měření konečného sestrojeného výsledku není důkaz správnosti konstrukce. Ze správnosti konstrukce plyne, že naměříme správné hodnoty, opačná implikace však neplatí. Mohlo se stát, že jen konkrétní hodnoty v příkladu napomohly tomu, že zkonstruovaný výsledek vypadá úplně stejně, jako kdybychom konstruovali správným způsobem.

Uvedu příklad:

Je dán konvexní čtyřůhelník ABCD. Sestrojte průsečík jeho úhlopříček.

Špatný postup, který ale např. pro speciální případ čtverce dá správný bod (tzn. měřením se nepozná, že je postup špatný):

"Sestrojíme kolmici p na stranu AB procházející středem AB. Dále sestrojíme rovnoběžku q se stranou AB, která prochází středem strany DA. Průsečík p a q je pak průsečík úhlopříček."

Např. pro kosočtverec je tento bod zřejmě odlišný od průsečíku úhlopříček.

Ivana · 01. 01. 2009 20:36

↑ DragonX:Každopádně dej pak vědět ,jak jste to řešili ve škole .

Ivana · 01. 01. 2009 20:45

↑ BrozekP:
Já jsem to pochopila tak, že body UV jsou dány v zadání. Bod V jsem sestrojila tak, že.... raději to pošlu skenem :

DragonX

ještě bych měl jeden dotaz... profesorka nám přes vánoc dala papír s příkladama a jeden je tu

Do daného rovnoběžníku KLMN vepište čtverec ABCD tak, aby $A \in KL, B \in LM, C \in MN, D \in KN$

ale do rovnoběžníku přece čtverec nevepíšu?

zkoušel jsem to otočením o 90° ale to jde jen u kosočtverce u obyčejného rovnoběžníku to přece nejde?

Ivana · 01. 01. 2009 21:12

↑ DragonX:

Kosočtverec je přece také rovnoběžník :-) .. termín obyčejný rovnoběžník neznám..

Jinak kosočtverec a kosodélník , čtverec, obdélník .. jsou rovnoběžníky a zároveň jsou to čtyřúhelníky.

Ivana · 01. 01. 2009 21:19

↑ DragonX:
A ještě doplním : lichoběžník je sice čtyřúhelník, ale už to není rovnoběžník .

DragonX · 01. 01. 2009 21:21

↑ Ivana:
Obyčejným rovnoběžníkem jsem myslel že není pravoúhlý jako čtverec a obdélník nebo tak :-)

Ivana · 01. 01. 2009 21:45

↑ DragonX:Já rozumím , ale ten termín není úplně správný. To už spíš ,že obdélník nebo čtverec jsou pravoúhlé rovnoběžníky.

Pavel Brožek

↑ Ivana:

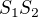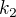Body U a V v zadání nejsou, ale už je jasné jak je sestrojuješ. Jestli to dobře chápu, tak pak sestrojíš kolmici l na přímku $S_1S_2$ vzdálenou a od $S_2$ . Průsečík l a $k_2$ označíš Y. Pak už mi tvůj postup není vůbec jasný (vypadá to, že už pouze sestrojíš rovnoběžku s p procházející Y a tou jsou dány tětivy, ale to by pak nedávalo smysl, proč posouváš bod Y do bodu Y'), tak prosím pokračuj, případně i oprav, co jsem napsal.

Ivana · 02. 01. 2009 09:41

↑ BrozekP:
Pokračovat budu to samozřejmě ,...
....tak tedy hledala jsem vektor , podle kterého jsem pak posunula bod $Y$ , který leží tak, jak jsem naznačila v konstrukci....
Máš pravdu, že pak už jsem jen vedla přímku $q$ rovnoběžnou s přímkou $p$ . To odpovídá zadání...
V podstatě mi nezbývá než s tebou souhlasit.
Hledala jsem zadání v uč.Planimetrie pro gymnásia a nenašla jsem jej.. ,ale nevadí.
Myslím si , že existuje jen to jedno řešení.
To by pak znamenalo , že stačí najít jen jeden bod ... já jsem zvolila ten bod $Y$ .(protože směr mám daný tou úsečkou $UV$ ).
Někdy se v těhle úlohách postupuje tak, jakoby již úloha byla vyřešena a pak se hledá vektor, podle kterého přenesu alespoň jeden bod. Proto jsem takto postupovala. Asi je to nesrozumitelně napsané , ale ještě na tom budu pracovat. :-)

jelena · 02. 01. 2009 10:32

↑ Ivana:

Ivano, zdravím srdečně :-)

Ty víš, jaký vztah mám ke konstrukčním úlohám :-(

Jen takové poznámky:

- v zadání je vzdálenost středu kružnic od přímky p - je potřeba sestrojit přímku p a kolmici k přímce p a zakreslit ekvidistanty (rovnoběžky ve vzdálenosti 5 cm a 4 cm). S1 se vyznačí na ekvidistantě 5 cm libovolně, poté ze středem v bodě S1 sestrojime kružnici o poloměru 4 cm - tam, kde se kružnice protne druhou ekvidistantu, tam máme bod S2 (to jen pro upřesnění vychozího zadání). - to poznámka k obrázku ↑ Ivana:. Když sestrojime nejdřív vzdálenost středu, tak bychom museli použit zcela jiný postup pro "dokreslení přímky p".

- při rozboru by se měla situace zakreslit tak, že předpokládáme, že úloha je vyřešena a hledáme, jaká cesta k tomu mohla dovést.

- požadavek, aby tětivy byly shodné se rovná požadavku sestrojení shodných úseček. Úsečky nemáme, ale víme, že konce úseček leží na zadaných kružnicích. Z napovědy (užití posunutí) odvodíme, že posouváme kružnici k1 tak, aby jeden konec hledáné úsečky, ležicí na k1 se společně s k1 posunul na k1´ a zároveň se "dostal" na k2.

Abychom posunuli kružnici k1, stačí posunout jeji střed - vektor posunutí použijeme ten, jak je uvedeno v nápovědě od ↑ BrozekP:. Vznikne společný bod obrazu k1´ a k2 (bod Y), přes neho pak vedeme přímku rovnoběžnou se zadanou p a hledáme průsečiky přímky q a kružnic k1, k2.

Obdivuji Tvoji geometricko-konstrukční vytrvalost a přeji hodně zdaru ve všem po celý rok :-)

Matematické Fórum

#1 31. 12. 2008 00:06

Planimetrie

#2 31. 12. 2008 19:40

Re: Planimetrie

#3 01. 01. 2009 14:03 — Editoval DragonX (01. 01. 2009 14:27)

Re: Planimetrie

#4 01. 01. 2009 17:57

Re: Planimetrie

#5 01. 01. 2009 18:03

Re: Planimetrie

#6 01. 01. 2009 18:05

Re: Planimetrie

#7 01. 01. 2009 18:10

Re: Planimetrie

#8 01. 01. 2009 18:30

Re: Planimetrie

#9 01. 01. 2009 18:47

Re: Planimetrie

#10 01. 01. 2009 18:58

Re: Planimetrie

#11 01. 01. 2009 19:07

Re: Planimetrie

#12 01. 01. 2009 19:33

Re: Planimetrie

#13 01. 01. 2009 20:17

Re: Planimetrie

#14 01. 01. 2009 20:35

Re: Planimetrie

#15 01. 01. 2009 20:36

Re: Planimetrie

#16 01. 01. 2009 20:36

Re: Planimetrie

#17 01. 01. 2009 20:45

Re: Planimetrie

#18 01. 01. 2009 20:50 — Editoval DragonX (01. 01. 2009 20:54)

Re: Planimetrie

#19 01. 01. 2009 21:12

Re: Planimetrie

#20 01. 01. 2009 21:19

Re: Planimetrie

#21 01. 01. 2009 21:21

Re: Planimetrie

#22 01. 01. 2009 21:45

Re: Planimetrie

#23 02. 01. 2009 02:01 — Editoval BrozekP (02. 01. 2009 02:03)

Re: Planimetrie

#24 02. 01. 2009 09:41

Re: Planimetrie

#25 02. 01. 2009 10:32

Re: Planimetrie

Zápatí