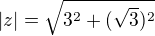Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Goniometrický tvar komplexního čísla (TOTO TÉMA JE VYŘEŠENÉ)
#1 06. 04. 2013 17:24 — Editoval dorfik (06. 04. 2013 17:27)
Goniometrický tvar komplexního čísla
Zdravím,
učím se a učím a najednou narazím na problém :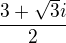
vyjde mi 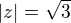 , tak, že
, tak, že 
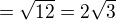
no a teď nevím co s tou 2 ve jmenovateli, takže jsem to tím vydělil.. vyšlo mi tedy 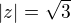 což má být správně..
což má být správně..
ale když dále počítám 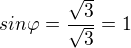
ale mělo by vyjít 
nedokáži si to nějak zdůvodnit..
děkuji za reakce :)
Offline
- (téma jako vyřešené označil(a) dorfik)
#5 06. 04. 2013 17:41
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: Goniometrický tvar komplexního čísla
↑ dorfik:
Už v té absolutní hodnotě máte zmatek. Nejprve máte výsledek 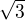 a potom
a potom 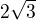 .
.
Chybu děláte v tom, že jste špatně určil reálnou a imaginární složku komplexního čísla. Proto jsem to napsal rozepsané. Tak pro jistotu ještě jednou: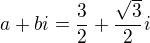 Kolik je a a b?
Kolik je a a b?
Offline
#8 06. 04. 2013 17:57 — Editoval teolog (06. 04. 2013 17:57)
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: Goniometrický tvar komplexního čísla
↑ dorfik:
Dosadíte do vzorečku, pro cos dosadíte reálnou část a vydělíte to tou absolutní hodnotou.
1) Jenže vám ta absolutní hodnota vyšla 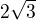 , což ukazuje nějakou chybu. Sice jste to vydělil dvojkou, aby to vyšlo, ale takto se absolutní hodnota nepočítá.
, což ukazuje nějakou chybu. Sice jste to vydělil dvojkou, aby to vyšlo, ale takto se absolutní hodnota nepočítá.
2) Kolik je ta reálná část zadaného komplexního čísla?
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Goniometrický tvar komplexního čísla (TOTO TÉMA JE VYŘEŠENÉ)
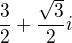 .
. mám problém..
mám problém.. 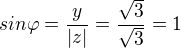
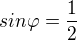
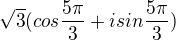
 a
a 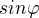 .. ?
.. ?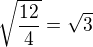
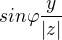 jsem místo
jsem místo 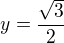 dosazoval pouze
dosazoval pouze